|
The purpose of this study is to explore Grade 9 learners’ understanding of ratio and proportion. The sample consists of a group of 30 mathematics learners from a rural school in the province of KwaZulu-Natal, South Africa. Data were generated from their responses to two missing value items, adapted from the Concepts in Secondary Mathematics and Science test set in the United Kingdom over 30 years ago. The study utilised Vergnaud’s notion of theorems-in-action to describe the learners’ strategies. It was found that the most common strategy was the cross multiplication strategy. The data reveal that the strategy was reduced to identifying and placing (often arbitrarily) three given quantities and one unknown in four positions, allowing the learners to then carry out an operation of multiplication followed by the operation of division to produce an answer. The study recommends that the role of the function underlying the proportional relationship should be foregrounded during the teaching of ratio and proportion.
There have been numerous studies focused on ratio and proportion which have looked at learners’ strategies and errors (Ben-Chaim, Keret & Ilany, 2012; Chick & Harris, 2007; Jiang, 2008; Lamon, 2007; Long, 2011; Md-Nor, 1997; Misailidou & Williams, 2002; Olivier, 1992). Many researchers agree that understanding proportional relationships is a long-term developmental process (Ben-Chaim et al., 2012) and forms a fundamental building block for many other areas in mathematics as well as in the sciences. Many phenomena studied in daily life, physics, chemistry, biology, geography, agriculture, woodwork and needlework and economics are defined using proportion (Ben-Chaim et al., 2012; Olivier, 1992). It is evident that a poor understanding of proportion can limit a learner’s access to various concepts and subjects.
This article reports on part of a bigger study which investigated Grade 9 learners’ understanding of ratio and proportion (Mahlabela, 2012). The bigger study used eight test items adapted from the original Concepts in Secondary Mathematics and Science study (Hart, 1981). In this article we report on the strategies and errors exhibited by the learners in two of these items, which consist of missing value problems where three quantities are given and the task is to find the fourth one.
|
Strategies used in solving missing value problems
|
|
To understand learner errors, one has to look at the methods or strategies that the learners use to arrive at the incorrect solutions. Errors could be the results of incorrect strategies or the results of incorrect use of correct strategies. Some strategies identified in the literature are now briefly described.
The for every strategy entails finding the simplest ratio first and then multiplying by a factor that yields the required result. The unit value strategy is similar except that the simplest ratio is reduced to a unitary ratio. This strategy has been identified in studies conducted in various countries (Hart, 1988; Jiang, 2008; Md-Nor, 1997; Misailidou & Williams, 2003).
The multiplicative strategy (within measure space approach) entails determining a ratio of measures from the same space and using it as a factor (Hart, 1988; Md-Nor, 1997; Misailidou & Williams, 2003).
The cross multiplication strategy based on setting up a proportion is also described as the rule of three by some (Md-Nor, 1997; Vergnaud, 1998) or algebraic method (Jiang, 2008) or the use of the formula x/a = y/b (Hart, 1984; Olivier, 1992).
In the constant difference or incorrect addition strategy or additive strategy, the relationship within the ratios is computed by subtracting one term from another and then applying the difference to the second ratio (Hart, 1988; Md-Nor, 1997; Misailidou & Williams, 2003).
According to Misailidou and Williams (2003) the additive strategy is the most commonly reported erroneous strategy in the research literature. Long (2011) made a similar finding in the Trends in International Mathematics and Science Study (TIMSS) with South African learners.
The building-up strategy involves establishing a relationship within a ratio and then extending it to the second ratio by addition (Md-Nor, 1997, p. 34) and is also referred to as the addition and scaling strategy (Hart, 1988), because it involves a multiplicative strategy combined with an additive one.
The incomplete strategy (Misailidou & Williams, 2003) involves using the same number given for the measure space. Long (2007) found that in TIMSS some responses were incorrect because of ‘incomplete reasoning’. She says that learners’ ‘reasoning took them part way towards the answer’ (p. 16).
An incorrect strategy is the incorrect doubling method. Since there are problems involving ratio and proportion where doubling is a correct strategy, the word ‘incorrect’ signals that the use of doubling was wrongly implemented in the setting.
|
A framework for understanding ratio and proportion
|
|
Researchers (Ben-Chaim et al., 2012; Olivier, 1992; Vergnaud, 1998; Wu, 2006) point out that proportional reasoning is just mathematical reasoning based on the concept of a linear function without a constant term.
Proportional reasoning requires a recognition that a situation is completely described by a function of the form shown in Equation 1:
Knowing  for all x implies that for any two non-zero values x1 and x2, Equation 2 is true: for all x implies that for any two non-zero values x1 and x2, Equation 2 is true:
We say the four numbers f(x1), x1, f(x2) and x2 form a proportion which can be expressed in terms of ratios: f(x1): x1 = f(x2): x2.
The proportional relationship can also be written as Equation 3:
Equivalently, it can be expressed as the ratio representation x2:x1 = f(x2):f(x1).
The relationship expressed in Equation 2 is such that the two quantities forming the fraction are from different measure spaces; this expression is referred to as a rate and the value is actually the constant coefficient (Vergnaud, 1998) or the constant of proportionality, c, from Equation 1. The term measure spaces is used by Vergnaud to express the fact that certain quantities belong to one measure space, which may have particular measures of, for example, length or cost, and others belong to a second measure space, which may have dimension of weight, distance or length, for example.
Considering Equation 3, we note that the fraction formed by the two quantities in each case has no dimension because they are from the same measure space. Vergnaud (1998) refers to this as a scalar fraction. Hence, the proportional relationship can be expressed as an equality between two rates (Equation 2) or as an equality between two scalar fractions (Equation 3).
Vergnaud (1998) uses the term theorems-in-action to describe the cognitive processes and yet-to-be concepts of a learner. A theorem-in-action is the set of mathematical relations considered by learners when they choose an operation or a sequence of operations to solve a problem. These theorems are implicitly held by learners and may not be articulated. Sometimes these theorems-in-action are not correct, but they can help teachers and researchers to analyse learners’ intuitive strategies and give insight into their thinking. Long (2011, p. 109) asserts that identifying ‘theorems-in-action provides a way to make a better diagnosis of what students know and do not know’.
An important property of the linear function f(x) is described by Equation 4:
Vergnaud (1998) draws on this property to illustrate learners’ implicit theorems-in-action when solving a problem based on a train travelling at constant speed, which took 16 minutes to travel 40 km from Town A to Town B. Learners were asked for the distance between Town B and Town C, given that it took the train 36 minutes to travel from Town B to Town C.
A learner wrote: 40 × 2 = 80; 80 + 10 = 90. Vergnaud explains that 36 minutes can be decomposed into 2 × 16 minutes + 4 minutes, and 4 minutes = ¼ of 16 minutes. Therefore, the corresponding distance is 2 × 40 km + ¼ of 40 km.
Note that one can manipulate Equation 4, to derive a further property used by Vergnaud (1998), that is f(m.1) = c(m.1) = c.m = f(1).m = m.f(1), thus leading to  , and hence to Equation 5: , and hence to Equation 5:
where m is any real number
Vergnaud describes another way of solving proportionality problems, which he calls the rule of three. Equation 6 follows directly from Equation 3:
In Equation 6, f(x1), x1 and x2 are known and f (x2) is required.
This qualitative study was conducted with a group of 30 Grade 9 learners from one school in KwaZulu-Natal, South Africa. The school is situated in a rural area, with most learners coming from impoverished backgrounds. The school was selected because of its proximity to the authors, which can be described as convenience sampling. Ethical requirements were fulfilled according to the ethical procedures stipulated by the local university.
The original larger study (Mahlabela, 2012) used eight questions that were adapted from the Concepts in Secondary Mathematics and Science study. However, in this article we only report on learners’ responses to two items, because of the variety of rich responses that emerged from these. After an initial marking and coding of the scripts, five learners were identified and selected for semi-structured interviews. Learners are referenced as Learner 1 to Learner 30, according to the order in which the scripts were collected; the numbering does not denote any difference in ability between the learners. The research questions that underpin this study are:
- What strategies do learners use to solve the two test items?
- What are the underlying theorems-in-action associated with these strategies?
- What do the theorems-in-action suggest about the learners’ understanding of ratio and proportion?
The learners’ written responses were analysed by studying their final answers and their working details to identify the strategy that was used. In some cases we were unable to identify a definitive strategy and this was described as ‘miscellaneous’. Interview responses helped to support our strategy classification.
Performance on Question 1
Learner responses are analysed separately: Question 1a and Question 1b first and the rest later. Table 1 shows how learners responded to Question 1a and Question 1b; Table 2 shows performance in the rest of the questions.
| TABLE 1: Learner responses to Question 1a and Question 1b (N = 30). |
 |
FIGURE 1: The onion soup recipe (Question 1). |
|
 |
FIGURE 2: Response of Learner 13 to Question 1a. |
|
One way of solving Question 1a and Question 1b would be to halve the ingredients in the given recipe since soup is being prepared for four people. More than 70% of the participants responded correctly to both questions. Some learners used the incorrect strategy of incomplete halving, where they just indicated that they needed half of the ingredients given in the recipe, but did not work out what half the actual amounts were.
Other errors were related to incorrect cross multiplication as some learners obtained the solution of 4 in Question 1a as shown in Figure 2.
Learner 13 omitted an equal sign between the equivalent fractions. The ratio of people in the two recipes (given recipe for eight people and the recipe for four people) is 8:4, which the learner wrote as (8 people)/(4 people). The ratio of water amounts is 2:x, where x is the amount of water needed to make soup for four people. She correctly formulated the two scalar fractions described in Equation 3 by comparing quantities from the same measure space (i.e. quantities of the same kind or elements of the same set). To find the amount of water needed (value of x), she multiplied 8 (the number of people given in the recipe) by 2 (the amount of water needed to make the soup for eight people) and then divided the product by 4 (the number of people that soup was needed for). We refer to this error as incorrect cross multiplication. The learner explained her method of cross multiplication and, interestingly, provided an explanation different from the written one appearing in Figure 2:
| Interviewer: |
I can see that your answer to this question is 4 pints. Tell me how you got 4 pints? |
| Learner 13: |
I took 8, the number of people in the recipe and wrote it down. I then took 2, the number of pints needed to make soup. I wrote 8 over 4, the number of people that I want to make the soup for. Because I do not know the number of pints of water needed, I wrote over x [the unknown]. I then cross multiplied. I got 8x and 8. I divided by x, although I am no longer sure this is how I did the calculation [she realises that this solution is different from the one which appears on the script]. I then wrote x and moved 8 to the other side [as if she has the equation 8x = 8]. |
Learner 13 in her written response in Figure 2 seemed to confuse cross multiplication with the rule for multiplication of fractions, that is, multiplying the numerators of the scalar fraction to get the numerator in the answer and multiplying denominators to get the denominator in the answer (however the confusion is not exhibited in her interview). A perusal of the learner scripts revealed that the error in Figure 2 recurs in other solutions obtained using this strategy.
One way of solving Question 1d and Question 1e would be to halve (to obtain ingredients for four people), halve again (obtain ingredients for two people) and then add the result to the first halving to find the ingredients required for 6 people – called the build-up strategy. For example, to determine the amount of water needed to make soup for six people, learners could halve 2 pints of water (water needed to make soup for eight people) to get 1 pint (amount of water needed to make soup for four people). They could halve 1 pint of water again to get ½ pint (amount of water needed to make soup for two people). The amount of water needed to make soup for six people is then 1 pint of water + ½ pint of water = 1½ pints of water.
The problems could also be solved by the use of the for every strategy or the multiplicative strategy. The performance of learners is shown in Table 2.
Over half (60%) of the learners answered Question 1c correctly, more than 66% correctly answered Question 1d, but only 10% answered Question 1e correctly. This is not surprising as Question 1e required halving and addition of fractions whilst Question 1d required halving and addition of whole numbers and Question 1c required halving of whole numbers and addition of a whole number to a fraction.
The incomplete use of the build-up strategy (incomplete build-up strategy) was observed in all three questions. In Question 1c, for example, 6% of the learners either halved once to get 1, or halved twice to get ½ Learners who halved twice did not add the first answer to the second answer. Many learners also used an incomplete strategy (using the same number given for the measure space). For example, in Question 1e it is stated that ½ pint of cream was needed to make soup for eight people. About 13% of the learners said that ½ pint of cream was needed to make soup for six people too. Some strategies were based on incorrect cross multiplication.
Other incorrect answers obtained by the learners, categorised as ‘other’, were diverse. The solutions emanated from the incorrect performance of either basic operations, conversions from one unit to the other or both. For example, in Question 1d, learners divided 24 by 8 and obtained 2 as the quotient (computational error). In Question 1e, learners divided (½ × 6) by 8 and obtained 0,75 (computational error). Some learners found the product of 6 and ½ to be 7,2 (a computational error) and then some correctly divided 7,2 by 8 to obtain 0,9, whilst others divided 7,2 by 8 to obtain an incorrect answer of 9. In Question 1d one learner incorrectly converted ½ to a decimal as 1,5. To arrive at ½ in Question 1e, Learner 15 incorrectly answered as shown in Figure 3; this was categorised as an incomplete strategy. It however includes the same misconception as that displayed by Learner 13 in Figure 2, who multiplied fractions instead of ‘cross multiplying’ across an equal sign, because there was no equal sign between the fractions.
Learner 15’s response in Figure 3 shows that he has modelled the relationship correctly by mapping 8 people to 6 people and ½ pint of cream to the unknown volume of cream. However, by not expressing the relationship as equivalent fractions, the learner has taken this as a product of two fractions (similar to the misconception Learner 13 displayed in Question 1a). However, Learner 15 has furthermore ignored the unknown and carried out the computation with numbers only. A third error is that he has interpreted the quotient of (8 × 6) and ½ as 4 × 3, which represents two errors: taking divided by ½ as divided by 2 and also taking pq/2 as p/2 × q/2. Thus, there are many algebraic misconceptions in these few lines.
Performance on Question 2
The question in Figure 4, a version of Piaget’s popular eel question, was the second question in the research instrument.
Piaget’s eel question is concerned with the amount of food given to eels of different lengths, the amount being proportionate to the length of the eel (Hart, 1981). Table 3 shows the performance of learners for each sub-question.
 |
FIGURE 3: Response of Learner 15 to Question 1e. |
|
| TABLE 2: Learner responses to Question 1c–e (N = 30). |
More than 50% of the learners responded correctly to each sub-question, except in Question2d. The performance of learners in Question 2a was outstanding as 90% of the learners responded correctly to this sub-question.
Many errors in this question resulted from the incorrect use of cross multiplication strategy. Figure 5 shows how Learner 6 arrived at the incorrect answer of 25 sprats in Question 2a(i). Learner 6 used the equal sign incorrectly by expressing equality between quantities from two different measure spaces (2 sprat = 5 cm and x sprats = 10 cm). In order to apply the cross multiplication strategy, two equivalent rates or scalar fractions would be needed, which Learner 6 did not identify correctly. In fact, the result was obtained by multiplying the length of eel A (5 cm) by the length of eel B (10 cm) and then dividing the product by 2 (the number of sprats that A is fed with).
The responses of Learner 17 (see Figure 6) indicate the use of the cross multiplication rule. However, the choice of which of the available numbers should be the multipliers and which should be the divisor seems to systematically follow a set formula. In the first case it was that the number of sprats for eel  ; this was similar in each case. Learner 17 has thus consistently used the cross multiplication rule as ; this was similar in each case. Learner 17 has thus consistently used the cross multiplication rule as  , where x is the length of the eel and f(x) is the number of sprats fed to the eel. , where x is the length of the eel and f(x) is the number of sprats fed to the eel.
 |
FIGURE 5: Response of Learner 6 to Question 2a(i). |
|
 |
FIGURE 6: Response of Learner 17 to Question 2. |
|
| TABLE 3: Learner responses to Question 2 (N = 30). |
Note that at no point in these or any other solutions which used the cross multiplication rule was there a point where any learner expressed equality between two scalar fractions or two rates. For example, consider the response of Learner 14 to Question 2 in Figure 7. The learner has modelled the situation correctly by associating the quantities from one measure space to the next, in the correct order, for each of the questions. She then carried out a cross multiplication across the vertically opposite numbers and created an equation in each case which she then solved correctly. All of these steps were done four times, without once expressing an equation in the form of Equation 2 or Equation 3, without which none of these relationships holds true. The fact that none of the learners expressed such equations suggests that they were influenced by teaching methods.
The incorrect addition strategy was also observed in learner responses. Participants suggested that the eels should be given two more or fewer sprats or fish fingers, depending on the length of the eel. Actually the addition strategy leads to the correct answer for Question 2a. If eel A is fed two sprats, then eel B should be given two more sprats, because eel B is twice the length of eel A. However, the strategy does not work for other sub-questions. When used in Question 2b, it yields an incorrect answer of 14 (obtained by 10% of the participants). There were also instances where learners added or subtracted 5 (the difference in eel lengths). For example, an incorrect result of 17 sprats in Question 2b was obtained by adding 5 sprats to 12 sprats.
The incorrect doubling or incorrect halving strategy was also identified in some responses. The strategy works correctly in Question 2a(i), but immediately fails in Question 2a(ii), yielding an incorrect result of 8. The reason for the incorrect answer of 4½ in Question 2c is incorrect halving.
 |
FIGURE 7: Responses of Learner 14 to Question 2. |
|
Figure 8 illustrates correct and incorrect solutions, based on the unitary strategy from the script of Learner 16. Learner 16 divided or multiplied the eel length by the number of sprats or mass of fish fingers it is fed. She divided where the number of sprats or mass of fish fingers was given for a longer eel in order to find how much should be given to the shorter eel. To determine how much the eel should be given, its length should be divided by the quotient obtained during the first division. In Question 2c the longer eel is 15 cm. The eel is fed 9 sprats; hence, Learner 16 divided 15 by 9 and got 1,67. The length of eel B (10 cm) was then divided by 1,67. She obtained an answer of 5,99 which she then incorrectly rounded off to 5,10. The correct answer is 6.
Her attempts at Question 2d reveal her uncertainty. She first wrote 10 ÷ 2 = 5, followed by 25 ÷ 2 = 12,5 (instead of 25 ÷ 5, which is the quotient of the first answer). She then struck off the division signs, replaced them with multiplication signs and repeated the same method: 10 × 2 = 20, then 25 × 2 = 50. Similarly for Question 2e, she first wrote 15 ÷ 9 = 1,67 and 25 ÷ 1,67, which is correct. However, she then replaced this with 15 × 9 = 135 and 25 × 1,67 = 41,67. Learner 16 seemed to have confused herself about the operations that she needed to carry out.
A scrutiny of Question 2f shows that she seems to have worked through her confusion and presented the correct operations and sequence of operations as she did for Question 2c. However, she has made a slip and swopped the two solutions. That is, her response for Question 2f(i) is the solution to 2f(ii) and vice versa.
 |
FIGURE 8: Response of Learner 16 to Question 2. |
|
Additional information on learner errors was obtained through interviews. The interview with Learner 8 is now presented in three excerpts, each of which details a different strategy. The dialogue below (Excerpt 1) elaborates on how Learner 8 arrived at his solution for Question 2a:
| Interviewer: |
You said that if eel A gets 2 sprats, then eel B must get 4 sprats. … How did you arrive at that? |
| Learner 8: |
Eel A is 5 cm long, right. If eel A gets 2 sprats, then eel B gets 4 because 5 is half of 10. So if eel A gets 2, eel B gets 4. |
| Interviewer: |
If A gets 3? |
| Learner 8: |
Then B gets 6. |
Learner 8 seems to recognise proportion very well in this problem. He realised that eel B is double the length of eel A and therefore should get double the number of sprats given to eel A.
The conversation (Excerpt 2) continued by looking at Question 2b as follows:
| Interviewer: |
If eel B gets 12 sprats how many should eel A get? |
| Learner 8: |
If eel B gets 12 sprats, then eel A should get 6. |
| Interviewer: |
Good. If eel B gets 12 sprats, you said in your script eel C gets 24 sprats. How did you get 24? |
| Learner 8: |
24? I was in a rush then, I must have said 12 × 2 and got 24. I should have said if B gets 12, C gets 30. |
| Interviewer: |
30? … How did you get 30? |
| Learner 8: |
I said 15 × 2. |
| Interviewer: |
Why did you say that? |
| Learner 8: |
Eel C eats more than eel B. |
| Interviewer: |
More? |
| Learner 8: |
Yes. |
| Interviewer: |
Why do you multiply by 2? |
| Learner 8: |
I was in a hurry and the bell was ringing. |
In Excerpt 2, Learner 8 multiplied 12 by 2 to get 24 and multiplied 15 by 2 to get 30, showing that he has now tried to extend the doubling strategy which yielded the correct answer in Excerpt 1. However, doubling does not work in this case. He seems convinced that eel C should get twice what eel B gets. The continuation of the conversation (Excerpt 3) now reveals a different strategy to Question 2d:
| Interviewer: |
Let us look at this one [Question 2d]. You said that if eel X gets 2 grams fish fingers, eel Z must get 7 grams. How did you get 7? |
| Learner 8: |
I added 5. |
| Interviewer: |
OK. You said if eel X gets 2 grams, eel Z gets 2 + 5 grams? |
| Learner 8: |
I said 2 + 5 and got 7. |
| Interviewer: |
Where did you get 5 from? |
| Learner 8: |
I said 25/5 and got 5, then here I said 2 × 5 to get 10 [length of eel X] and if I multiply 5 by 5 I get 25 [length of eel Z] over here. |
| Interviewer: |
Here [pointing at the learner working] you multiplied 5 by 2 and here you multiplied 5 by 5? So when you get 2 you add 5? |
| Learner 8: |
Yes, and I got 7. |
The conversation with Learner 8 in Excerpt 3 reveals that he has used an incorrect additive strategy: adding 5. However, his explanation is interesting. He correctly identified that the eel lengths are multiples of five with eel X being the second multiple of 5 (2 × 5) and eel Z being the fifth multiple of 5 (i.e. 5 × 5). However, having identified that the length of eel Z was the fifth multiple of 5, he then added the 5 to the 2 (from number of sprats that should be fed to eel X. He has not realised that he had obtained the required answer of 5. Note that Learner 8 has described three different strategies in the three excerpts of the interview, showing his uncertainty about the underlying relationships.
A conversation with Learner 27, who also used an additive strategy, went as follows:
| Interviewer: |
Let us look at this one [Question 2d]. Eel X is given 2 grams of fish fingers. How did you get the answer that eel Z should get 8 grams of fish fingers? |
| Learner: |
If I give eel X 2 grams, then I must give eel Y 4 grams, looking at how their lengths differ [observing a pattern of lengths]. I saw the lengths were 10, 15 and 20. I think I did not see that eel Z is 25; I think eel Z was supposed to get 8 grams if its length was 20 [seems to be trying to establish a pattern of 2, 4, 8 for eels X, Y, Z respectively]. I was not supposed to give eel Z 8 grams. I was supposed to give eel Z 12 grams. |
| Interviewer: |
Now your pattern is 2, 4, 8 for 10, 15, 20. Why is it not 2, 4, 6, 8? An eel of length 20 would get 6 grams and it would make sense to give eel Z 8 grams. |
| Learner: |
Actually I think that is exactly what I did. |
Learner 27 suggests that he tried to establish a pattern based on repeated addition, that is forming an arithmetic sequence. For eel length, he saw patterns or addition by 5. For fish finger mass the learner saw patterns of addition by 2.
The study found that learners used various strategies. There was also evidence that learners shifted between strategies, using different ones for the same question as Learner 13 and Learner 8 revealed in their interviews. This tendency demonstrates their uncertainty about the underlying relationships, which led them to adopt different ‘methods’ at different times because the methods seem arbitrary and are not grounded in the properties of the proportional relationship.
Learners often used incorrect mathematical notations such as 2 sprats = 5 cm (e.g. Learner 6 in Figure 5). This suggests little comprehension of what a proportional relationship entails. Learners’ misconceptions about number and algebra added to their confusion as was the case with Learner 15 in Figure 3, who displayed multiple errors, such as multiplying the equivalent fractions as well as incorrectly simplifying  to to  . .
The underlying theorems-in-actions associated with the strategies are now presented. The analysis of the underlying theorem-in-action is a tool that can be used to check the validity of a particular strategy and also helps us identify the scope and limits of application of a strategy.
The use of the doubling and halving strategies
It seems as if many learners recognised that some problems could be solved by halving or doubling or a combination of the operations. This implies that the operations were intuitive efforts in trying to obtain fitting answers. However, many of them performed incorrect operations or stopped short of completing all the steps. Most learners were able to solve Question 1a and Question 1b, which required just one operation of halving correctly, whilst some learners recognised the need for halving but did not know which quantity to halve. Doubling also led to the correct answer for Question 2a(i), which is discussed under additive strategies. The underlying theorem-in-action based on Equation 4 is that f(½ x) = ½ f(x) or f(2x) = 2f(x), which can yield the correct answer to the given proportionality problems. However, some learners may have doubled the elements across a measure space, such as Learner 8 in interview Excerpt 2, who doubled the length of the sprat Y and expressed it as the number of fish fingers required for Y. At other times learners doubled or halved quantities in the same measure space inappropriately such as those who used the halving strategy incorrectly in Question 2c.
Additive and subtractive strategies
Some learners resorted to addition or subtraction, which was incorrect in many cases. However, addition using the build-up strategy can lead to the correct answer. For example, Question 1e could be solved by first reducing the given ingredients by two factors and then adding the results. This is possible because  (using Equation 4, where x is the number of people and f(x) is the amount of cream needed for x people). (using Equation 4, where x is the number of people and f(x) is the amount of cream needed for x people).
Another instance when addition led to a correct answer was in Question 2a(i). The length of the eel increased from 5 cm to 10 cm. Hence the number of sprats increased from 2 to 4; this increase could be seen as an addition of 2. Here the function could be seen as  where x is the length of the eel X and f(x) is the number of sprats fed to eel X. Hence f(10) = 4 = 2f(5) = 2(2) which is also equal to 2 + 2. So this is true only because 2 + 2 = 2 × 2 in this instance. However in general, f(2x) ± 2 + f(x). where x is the length of the eel X and f(x) is the number of sprats fed to eel X. Hence f(10) = 4 = 2f(5) = 2(2) which is also equal to 2 + 2. So this is true only because 2 + 2 = 2 × 2 in this instance. However in general, f(2x) ± 2 + f(x).
For Question 2d Learner 8 used an incorrect additive strategy, as explained in Excerpt 2. He correctly identified that the eel lengths are multiples of five, with length of eel X being the second multiple of 5 and the length of eel Z being the fifth multiple of 5. Hence the number of fish fingers for eel X would be 2 (i.e.  then then  and the number of fish fingers for eel Z would be 5 and the number of fish fingers for eel Z would be 5  . However, having identified that the length of eel Z was the fifth multiple of 5, he then added 5 to the 2. He did not realise that he had obtained the required answer of 5. His solution can be expressed as f(z) = f(x) + fz), which does not hold in the case of a linear function unless x = 0 and f(x) = 0. . However, having identified that the length of eel Z was the fifth multiple of 5, he then added 5 to the 2. He did not realise that he had obtained the required answer of 5. His solution can be expressed as f(z) = f(x) + fz), which does not hold in the case of a linear function unless x = 0 and f(x) = 0.
Also in Question 2d, Learner 27 used an additive strategy in a different and also incorrect way. As the lengths of the lengths of the eels increased by 5 cm, in a corresponding manner he increased the number of fish fingers by 2. Hence, his incorrect solution can be expressed as f(x) = f(10) = 2, f(15) = f(10) + 2, f(20) = f(10) + 4; f(25) = f(10) + 6, statements which are not true.
Unitary strategy
In general there were few responses that indicated the use of the unitary method; however, Learner 16’s responses to Question 2c×2e are based on a version of the unitary method (Equation 5). However, it seems that he was uncertain about which operation to use and what the result of the operation represented. In working out 15 ÷ 9 = 1,67 for Question 2c the underlying theorem in action was  (Equation 5). That is, he worked out (Equation 5). That is, he worked out  . That is, . That is,  . He then went on to work out 10 ÷ 1,67 which is actually working out . He then went on to work out 10 ÷ 1,67 which is actually working out  , also using Equation 5, here where f(m) = 10, f(1) = 1,67 and m is unknown. So his method was correct; however, he entangled himself in trying to keep track of the operations and divisions and multiplications whilst also trying to identify which elements were from the different measure spaces. , also using Equation 5, here where f(m) = 10, f(1) = 1,67 and m is unknown. So his method was correct; however, he entangled himself in trying to keep track of the operations and divisions and multiplications whilst also trying to identify which elements were from the different measure spaces.
Cross multiplication strategy
Vergnaud refers to this strategy as the rule of three strategy. Suppose that the three quantities x1, x2 and f(x1) are given and f(x2) is required. Then, using Equation 2, we can follow five steps:
However, as shown in this study, even those learners who correctly carried out the strategy moved directly from step 1 to step 5, leaving all the intervening steps or transformations out. It is those omitted steps that demonstrate why the strategy works. In particular, it was noticed that learners expressed step 1 as step 1*, without using any equal or ratio sign:
Also, none of the learners expressed step 2 in their working details. Their strategy therefore was not based on knowledge of ratios and proportional relationships, but on meaningless operations of ‘cross multiply and divide’. Even the work of Learner 14 who arrived at the correct answers show that she moved directly from step 1* to step 5 without any of the intervening steps. This learner was able to consistently reproduce step 5 without including any of the transformations between step 1 and step 5, which is quite remarkable.
However, many of the other learners’ lack of knowledge of the specific transformations that make the cross multiplication rule work led to mistakes such as those demonstrated by Learner 13 in Question 1a, who formulated the correct relationship in step 1*, but who got confused when carrying out the operations and multiplied the scalar fractions 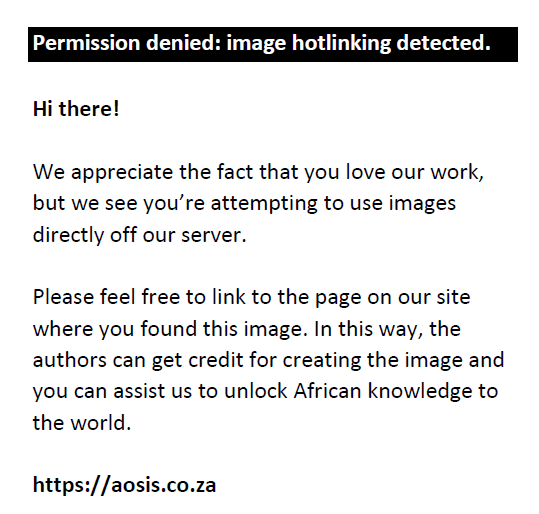 and and 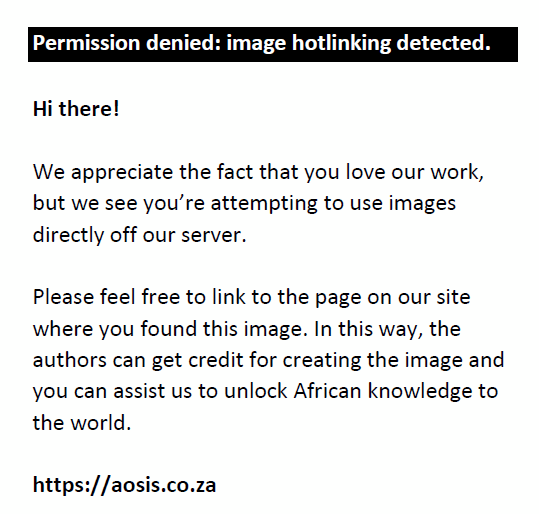 , where f(x) was the amount of water needed to make soup for x people. , where f(x) was the amount of water needed to make soup for x people.
Learner 15, in Figure 3, made a similar mistake, but his response suggested many other misconceptions besides the one held by Learner 13.
The errors displayed by Learner 17 in Question 2 can also be explained as incorrect application of the cross multiplication rule. Learner 17 only produced step 5 in each case of the form 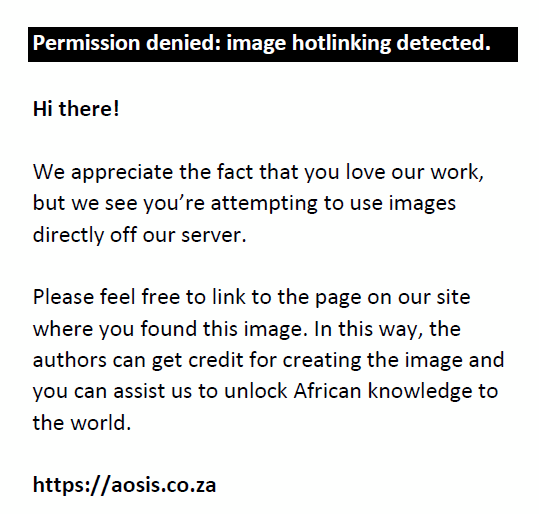 , instead of , instead of 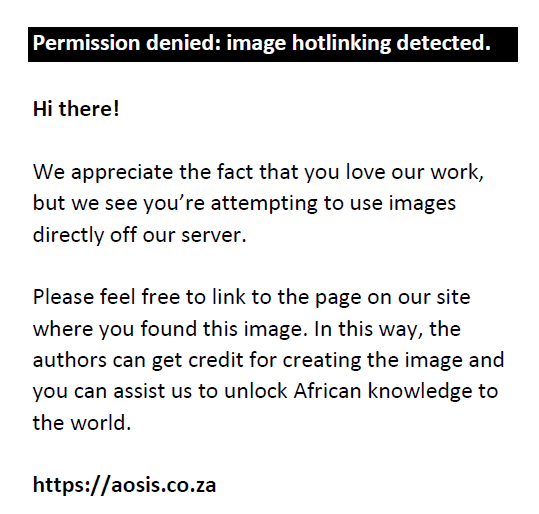 , which is the result of the correct application of the cross multiplication rule. , which is the result of the correct application of the cross multiplication rule.
These results support Olivier’s (1992) advice given more than 20 years ago that:
any teaching strategy which merely supplies pupils with recipes such as … cross multiplication and the unitary method which can solve certain classes of stereotypes proportional problems … cannot be effective. (p. 301)
Vergnaud (1998) notes in his study that only 1% of the participants used the rule of three, explaining that this low rate was because most learners consider that there is no meaning in multiplying quantities from different measure spaces (f(xi) x2).
Hart (1981) reports that ‘of the 2257 children … only 20 [15 from the same school] wrote down an equation of the form  and used it consistently and correctly’ (p. 89). ‘There was little evidence that the taught rule and used it consistently and correctly’ (p. 89). ‘There was little evidence that the taught rule  was remembered and used by children’ (p. 21). ‘Teaching an algorithm such as was remembered and used by children’ (p. 21). ‘Teaching an algorithm such as  is of little value unless the child understands the need for it and is capable of using it. Children who are not at a level suitable to the understanding of is of little value unless the child understands the need for it and is capable of using it. Children who are not at a level suitable to the understanding of  will just forget bd the formula’ (p. 101). will just forget bd the formula’ (p. 101).
In this study the cross multiplication method was the most common method, even though it is not an intuitive strategy. Of the 12 learners who showed some working details, all displayed evidence of using this strategy in their responses. It is therefore clear that the recipe for this method was taught to the learners, which many teachers under pressure may decide to do. However, not a single learner, even those who produced correct responses, were able to provide an explanation that showed reasoning beyond step 1*, suggesting that they did not know why the strategy worked. The cross multiplication strategy was clearly taught without ensuring an understanding of when and why it works; this effect was evident in the learners’ responses. It is acknowledged that the dynamics of the classroom are complex and often teachers face dilemmas about whether to teach for conceptual understanding or to focus on getting good results by focusing on procedures. However, teaching procedures without understanding, as alluded to by Olivier (1992) above, is not effective. In fact, this study shows that learning procedures without understanding the background does not even lead to good results.
In this article we analysed learners’ strategies to tackle questions based on ratio and proportion by identifying the underlying theorems-in-action. The identification of the theorems-in-action provided insight into whether their strategies were correct. This also helped us understand whether or not some incorrect methods produced correct answers coincidently because of the numbers that were used. As was shown, some of these incorrect theorems–in-action revealed procedural ways of working that contradicted properties of the direct proportional relationship. It was also shown that many learners opted for the cross multiplication rule; however, many were confused about which quantities should be the multipliers and which should be the divisor in the rule of three. We argue that the confusion emerged because none of the learners’ responses indicated Equation 2 or Equation 3, which are the crux of the proportional relationship. They then carried out operations without understanding the algorithm and why it worked. The number of possible permutations of four numbers in four positions is 4P4 = 24. Hence, there are 24 possible ways of arranging four numbers in terms of two equivalent fractions and only eight of them correctly represent the proportional relationship. In the absence of knowing the functional relationship that dictates exactly which fractions are equal, and why they are equal, learners seem to have guessed and placed the quantities (three given and one unknown) in arbitrary positions, allowing them to carry out the operations of ‘cross multiplication’ and division to arrive at an answer.
The study also found that no learner mentioned the words ratio or proportion. We can thus infer that most of these learners are working out the problems (some doing it successfully) without realising the meaning of equivalent ratios, or knowing the conditions under which four quantities form a proportional relationship. Hence they were carrying out the procedures without engaging with the linear function of the type y = kx, which defines the relationship between the quantities. The role of the function is not addressed, even in textbooks, and perhaps this omission is a large factor accounting for learners’ struggles with solving such missing value problems based on proportional relationships. Without reference to the linear function y = kx learners can rely only on memorised strategies. We therefore suggest that shortcuts such as the cross multiplication strategy should be not be used with secondary school learners without a concurrent emphasis on the role of the function that sets the conditions for the proportional reasoning.
Competing interests
The authors declare that they have no financial or personal relationship(s) that may have inappropriately influenced them in writing this article.
Authors’ contributions
The data collection and analysis was carried out by P.M. (University of KwaZulu-Natal). S.B. (University of KwaZulu- Natal) led the write-up of the article.
Ben-Chaim, D, Keret, Y, & Ilany, B.-S. (2012). Ratio and proportion. Research and teaching in mathematics teachers’ education (Pre- and in-service mathematics teachers of elementary and middle school classes). Dordrecht: Sense Publishers. http://dx.doi.org/10.1007/978-94-6091-784-4
Chick, H.L., & Harris, K. (2007, December). Pedagogical content knowledge and the use of examples for teaching ratio. Paper presented at the Annual Conference of the Australian Association for Research in Education, Fremantle, Australia. Available from http://www.aare.edu.au/data/publications/2007/chi07286.pdf
Hart, K.M. (1981). Children’s understanding of mathematics: 11–16. London: John Murray.
Hart, K.M. (1984). Ratio: Children’s strategies and errors. A report of the Strategies and Errors in Secondary Mathematics project. Windsor, Berkshire: NFER_NELSON.
Hart, K. (1988). Ratio and proportion. In J. Hiebert, & M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 198–219). Reston, VA: National Council of Teachers of Mathematics.
Jiang, C. (2008, August). Strategies for solving word problems on speed: A comparative study between Chinese and Singapore students. Paper presented at the 11th International Congress on Mathematical Education, Monterrey, Mexico. Available from http://tsg.icme11.org/document/get/773
Lamon, S.J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. In F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 1, pp. 629–668). Charlotte, NC: Information Age Publishing.
Long, C. (2007). What can we learn from TIMSS 2003? In M. Setati, N. Chitera, & A. Essien (Eds.), Proceedings of the 13th Annual Congress of the Association for Mathematics Education of South Africa (Vol. 1, pp. 1–23). White River: AMESA.
Long, C. (2011). Mathematical, cognitive and didactic elements of the multiplicative conceptual field investigated within a Rasch assessment and measurement framework. Unpublished doctoral dissertation. University of Cape Town, Cape Town, South Africa. Available from http://hdl.handle.net/%2011180/1521
Mahlabela, P.T. (2012). Learner errors and misconceptions in ratio and proportion: A case study of Grade 9 learners from a rural KwaZulu-Natal school. Unpublished master’s thesis. University of KwaZulu-Natal, Edgewood, South Africa. Available from http://researchspace.ukzn.ac.za/xmlui/handle/10413/6490/browse?value=Mahlabela%2C+Patisizwe+Tennyson.&type=author
Md-Nor, M. (1997). Investigation of the teaching and learning ratio and proportion in Malaysian secondary schools. In Proceedings of the British Society for Research into Learning Mathematics, 17(3), 32–37. London: British Society for Research into Learning Mathematics. Available http://www.bsrlm.org.uk/IPs/ip17-3/BSRLM-IP-17-3-Full.pdf
Misailidou, C., & Williams, J. (2003). Diagnostic assessment of children’s proportional reasoning. Journal of Mathematical Behavior, 22, 335–368. http://dx.doi.org/10.1016/S0732-3123(03)00025-7
Olivier, A.I. (1992). Developing proportional reasoning. In M. Moodley, R.A. Njisane, & N.C. Presmeg (Eds.), Mathematics education for in-service and pre-service teachers (pp. 297–313). Pietermaritzburg: Shuter & Shooter.
Vergnaud, G. (1998). A comprehensive theory of representation for mathematics education. Journal of Mathematical Behavior, 17(2), 167–181. http://dx.doi.org/10.1016/S0364-0213(99)80057-3
Wu, H. (2006, October) Professional development: The hard work of learning mathematics. Paper presented at the Fall Southeastern Section Meeting of the American Mathematical Society, Tennessee, USA. Available from https://math.berkeley.edu/~wu/hardwork2.pdf
|