|
This study used participant observation to explore students’ thinking when learning the concept of factorial functions. First-year university students undertaking a mathematics methodology course were asked to find the number of ways in which five people could sit around a circular table with five seats. Using grounded theory as a qualitative research strategy, we analysed student responses and written reflections according to the sequence of their experiential realities: practical and textual experiences. This was followed by an analysis of their reflections on both experiences in a pedagogical context. We found that the way basic mathematics operations are learned impacts on the student’s ability to experience components of new problems as familiar. Consequently, they encounter these problems as new and unfamiliar. At the same time we found that engagement with practical experience does allow for the emergence of representations that have the potential to be used as foundations for learning new and unfamiliar concepts. The blending of practical, textual and teaching experiences provoked students’ thinking and ultimately their understanding of a given new and unfamiliar mathematics concept.
|
Introduction and research questions
|
|
This article reports on an exploration of first-year university students’ (pre-service teachers) thinking in solving a factorial function problem. The role of the teacher in the activity was limited to presenting the situation and introducing some resources at different stages of the process. The reason for this was twofold: to introduce students to a different teaching approach in which learning is at the foreground and to introduce them to ‘pedagogical content knowledge’ (Shulman, 1986, p. 9). Two research questions emerged during the study, namely:
- What are the challenges associated with engaging in a self-directed learning activity of a new and unfamiliar mathematics concept?
- In what ways do pedagogical attributes affect learning of a new and unfamiliar mathematics concept?
The concept of the factorial function is associated with permutations, combinations, Stirling numbers and number theory (Bhargava, 2000). The factorial of a positive integer , denoted by , is the product of all positive integers less than or equal to . Symbolically, the function is defined by:
In the context of mathematics the definition and symbolic representations appear simplistic. Learners know how to multiply integers and rules of permutations and combinations can be easily followed. When the situation manifests itself in a real-world context, learners often encounter challenges, in particular with how one perceives continuous multiplication in a real-world context.
Malisani and Spagnolo (2009) attribute some of these challenges to the introduction of the concept of variables in the teaching of mathematics. They argue that ‘the concept of variable is used with different meanings in different situations’ (p. 21) and often unconsciously. This is a core problem in the growth of mathematics concepts. Skemp (1978) vividly demonstrates this in his conception of instrumental and relational understanding. Pirie and Kieren (1994) explore the same idea in their notion of growth in mathematical understanding. The phenomenon is adequately addressed by Tall (2008) in his characterisation of cognitive development through three worlds of mathematics. Lack of systematic development from one area of concept development and representation to another, as discussed by these three authors, often results in learning problems.
Elia and Spyrou (2006, p. 257) explicitly state that ‘the understanding of functions does not appear to be easy’. This is particularly so with the concept of factorial function as it requires the blending of different knowledge structures. Functions, especially in their symbolic form, are generalisations of relationships. Some studies, such as ones by Amit and Neria (2008) and Tarlow (2008), have reported that the ability to generalise and represent relationships requires higher order thinking skills, such as visualisation, holistic thinking, flexibility, reasoning and abstraction. Pure mathematics at university level tends to be taught within a formal framework of axiomatic systems and mathematical proof (Tall, 2008). Development of an understanding of mathematics concepts requires students to link ideas together for themselves and to take some responsibility for their own learning (Maoto & Wallace, 2006). Thus, the role of a teacher shifts to a facilitative one to allow students time to develop mathematical ideas rather than to impose those ideas onto them.
Most research in relation to the teaching and learning of the factorial function is covered in comprehensive studies that focus on combinatorics (Halani, 2013; Lockwood, 2011). Complex thinking processes are involved in learning combinatorics, including factorial functions. Lockwood (2011) presents two perspectives of thinking that underpin learning combinatorics: the process-oriented perspective and the set-oriented perspective. Meanwhile, Halani (2013) classifies the thinking that is involved in learning the factorial function into eight different categories: addition, union, standard odometer, wacky odometer, generalised odometer, deletion, equivalence classes and ratio.
Other researchers (Bintz & Moore, 2003; Braithwaite & Goldstone, 2013) focus on the teaching approaches that facilitate the learning of factorial functions. Bintz and Moore (2003) use specifically constructed stories that they read to their middle school learners to introduce factorials. In the context of university students, Braithwaite and Goldstone (2013) support an approach where what they term grounded representations precede formal representations.
The purpose of this literature review was not to identify gaps with respect to locating the study in literature. That would have defeated the grounded theory approach that we have adopted (Bitsch, 2005). Instead, we highlighted literature within which we could explain our emergent understandings of students’ learning of factorial function.
|
Theoretical and conceptual framework
|
|
Our emerging conceptualisation of the framework that best accounts for how the study unfolded and was processed and reported upon is informed by three theories: constructivism as a referent for teaching (Tobin & Tippins, 1993), theory of reflective practice (Schön, 1983) and grounded theory (Glaser & Strauss, 1967). Constructivism, when used as a referent (Tobin & Tippins, 1993), demands that students’ experiential reality provides a foundation upon which their knowing is constructed. Growth with regard to understanding of concepts is facilitated through a scaffolding process (Vygotsky, 1962). Schön’s (1983) idea of reflection-in-action is helpful with regard to how and when the knowledgeable other (Vygotsky, 1962) can provide timeous scaffolding.
The origins of grounded theory lie in Glaser and Strauss’s (1967) response to the dominant role theoretical frameworks have played in research, especially in the context of qualitative studies. According to Charmaz (2008), grounded theory ‘takes a systematic inductive, comparative, and interactive approach to inquiry’ (p. 156). Through this process ‘not only are the surprising data emergent, but the researcher’s theoretical treatment of them is also emergent’ (p. 157).
Our conceptualisation of the interrelationships of the three theories is captured in Figure 1.
In this model, the teaching and learning process unfolds first. The emerging data are analysed with the purpose of facilitating and supporting learning. The process is enriched by reflection-in-action. Where necessary, intervention in the process comes in the form of scaffolding. The interplay between emerging data, the results of reflection-in-action and scaffolding activities continues until the outcomes of learning are achieved.
Subsequently, grounded theory allows us to process the whole learning experience anew. The process is now guided by the need to understand what happened, focusing on the research outcomes. Research questions emerge and are pursued, guided by reflection-on-action (Schön, 1983). The process allows for the interrogation of the value of the questions that emerged during the facilitation of learning. Theoretical sampling, constant comparative analysis and emergence of categories or themes become realisable.
|
Research methodology and methods
|
|
This study was situated within the first author‘s own classroom, which consisted of 89 first-year university students who were registered for a mathematics methodology module. Data gathered in a setting where one could actually talk directly to participants, and see them behave and act within their context and ultimately reflect on their own learning, is a major characteristic of qualitative research (Creswell, 2007). Following the qualitative research strategy of grounded theory, data collection, analysis and interpretation proceeded interdependently and iteratively and was not influenced by the literature (Bitsch, 2005).
Data were mainly collected through submission of written responses, while participant observation during normal classroom interactions provided insights into the students’ responses. All 89 students worked in self-selected groups with a minimum of five members. The question given to them was: ‘In how many ways can five people sit around a circular table? Investigate and thereafter explain how you will teach this to Grade 9 learners’. Through the provision of scaffolding (Vygotsky, 1962), the students were expected to outline the key elements required to bring about an understanding of the activity and to clearly explain and justify their responses. On completion of their written responses, the students had to reflect on their use of mathematical strategies, mathematical processes and mathematical content, as well as reflect on the low and high moments they experienced. A day after their first submission they were given reference material which highlighted, in limited detail, linear and circular permutations, indicating symbolic generalisations of the two related functions. The intention was to scaffold the understanding and offer them an opportunity to attach meaning to, and to improve on, their initial explanations and justifications. It was also intended for the reference material to provoke their thinking towards generating functions for their different emerging sequence of numbers.
The written responses of the groups were submitted in three stages. The first set of responses were submitted immediately after practical experiences, the second set was submitted immediately after textual experiences and the last set came after students’ reflections on both experiences in a pedagogical context. During whole-class discussions, guided by their submitted responses at each stage, individual groups were asked to confirm the different interpretations that existed within and across the groups. It was this alternating between data collection and analysis that influenced how we organised and interpreted their findings. The back and forth experiences and reflective interpretations by both students and us provided a rich platform to trace students’ thinking towards an understanding of the problem. To back up the findings and discussions we used the exact final responses of the students without disclosing their identities, as agreed upon. In between the students’ quotes, we highlighted emerging lines of investigations and ideas that influenced students’ conclusions.
Ethical considerations
This qualitative study complied with all ethical requirements of the university. Approval was obtained from the department in which the study was located, the students and the relevant university structures beyond the department. The nature and purpose of the study were declared, inclusive of potential audiences and substantive foci. Erickson (1998, p. 1161) writes: ‘consent that is genuinely informed and without coercion reduces the risk of social harm because it affirms the dignity and respects the agency of those who will be involved in the study’. We agreed on anonymity of the participants, hence no individual identities were divulged during this study. The students themselves were beneficiaries of the results of this study. They were inducted into the dynamics of what it means to learn mathematics with a view to teaching young learners.
Quality criteria
The prolonged engagement (semester), persistent observation, ongoing probing during a number of whole-class discussions, peer debriefing and member checks provided enough opportunity to hear the students’ voices, which contributed to establishing credibility of this study (Bitsch, 2005; Guba & Lincoln, 1989). Recursive submissions from the students and sufficient descriptive data added to both confirmability and transferability of this study (Guba & Lincoln, 1989).
The practical interaction by the students with the task presented them with a unique learning experience, including counting of actual seating positions, engagement with some of the theories of counting presented in the handouts and the need to approach the task from the perspective of a teacher.
Each of these stages provided us with a glimpse into the thinking that students applied as they learned mathematics in the context of becoming teachers. In order to preserve the order through which the experiences unfolded, this section is presented in the three stages as they emerged: (1) practical experiences, representations and counting or enumeration strategies, (2) textual experiences, interpretations and applications and (3) reflections on both practical and textual experiences in a pedagogical context.
Practical experiences, representations and counting or enumeration strategies
The students’ engagement with the task involved talking about the task and using sketches on paper to determine the solution. Some students created the actual space in which seating would take place and exchanged seats, while other students recorded or counted the number of possible seating permutations. Lack of systematisation by students on how the activity was unfolding was apparent in the initial stage. However, over time, strategies became evident. Four different answers emerged, namely (1) 5 ways, (2) 20 ways, (3) 23 ways and (4) 25 ways in which five people could sit around a circular table. In almost all instances it was evident that the students considered the representation to be linear rather than circular. Each of these four different responses is examined in order of complexity.
Two groups of students gave an answer of five possible permutations, with the following explanations:
Firstly, each occupies a seat around the table. Then each moves to the next chair while the other one from right hand side moves to the chair left by the other. The one on the right hand side moves to make space for the other. At the end all five people would have occupied five chairs in different positions around that circular table.
There are 5 ways:
Letters of the alphabets represent names of people
The two strategies are clearly distinct and yet similar. In explanation 1 the focus is on each of the five people having an opportunity to occupy each of the five seats. The order in which they are seated remained static. However, it is still important that all of them are seated at the same time, though in different seats. Practical observations were used to arrive at the number of times this was possible.
Explanation 2 reflected a different strategy, where the students used the last five letters of the alphabet to represent people. This offered some systematisation of the process which was then used to visualise how five people could change their seating arrangements. The first and the last letters of the alphabet were systematically exchanged, leading to a total of five possible permutations of the seating arrangement. The relative positions of letters remained the same. V would always be next to and to the left of W, except when one of them is the last and the other is the first letter in the sequence. In the context of a circular table, the order of these letters remained the same. This makes the explanation similar to the first.
The difference between the two strategies is with regard to their potential in scaffolding towards the concept of factorial. The use of letters in explanation 2 allows for better manipulation.
The explanation of one group that arrived at this conclusion was:
If the first person occupied a position, the others can sit around 4 remaining positions. We say 4 ways for 1 person if stationary, therefore 5 people each with 4 ways: 5 × 4 to get 20 ways.
The strategy was to fix the first of the five positions while varying the remaining four; Halani (2013) calls that standard odometer thinking. This seating permutation could be achieved in exactly five different ways as there were five people. Once that was done, the remaining four positions produced four possible alternatives. While not explained by the students, this strategy of fixing of positions is similar to and enriches explanation 2 in response 1. This new thinking is an important aspect of the concept of factorial. Furthermore, the idea of expressing the numerical representation of fixing and varying seating positions through multiplication makes this an invaluable development in working towards the concept of factorial.
This response showed a two pronged strategy in which two different representations were used to arrive at 23 combinations. However, a closer review of the processes followed indicated that this group made an error and, in fact, the calculation leads to a total of 20 instead of 23 permutations. The explanation was:
1st position 5 candidates; 2nd position 4 candidates; 3rd position 3 candidates; 4th position 2 candidates; 5th position 1 candidate; added to the sequential positioning of 5 equals to 23 ways. Let’s say the candidates are named A; B; C; D; E
Sequential positioning equals 5 ways
The 1st is now last and so on
1st position: 7 ways; 2nd position: 5 ways; 3rd position: 3 ways; 4th position: 2 ways; 5th position: 1 way
Therefore 5 + 7 + 5 + 3 + 2 + 1 = 23 ways
The first strategy used considers the possibilities for each of the five seating positions. While this is still a feature of Halani’s (2013) odometer thinking, these positions were counted independently. The students did not consider the strings of seating arrangements that could arise from the approach. The subsequent possibilities of occupying a seat were not taken as linked to the previous possibilities. It is the absence of this connection that, we believe, makes the strategy ineffective. The second strategy was to use letters of the alphabet to represent different strings of seating arrangements. The sequence of the letters was maintained, unless subsequent letters were at the opposite ends of the string. The two strategies yielded 15 and 5 ways respectively leading to a total of 20 permutations. The 7 ways for the first position and the 5 for the second appear to be mistakes in the students’ work. Initially, the numbers were correctly given as 5 and 4. In terms of the ultimate purpose of engaging with the concept of factorial, the two strategies can be scaffolded for a successful count. The first strategy was, however, closer to the numerical and symbolic representation of the concept of factorial than the pictorial representation.
Two groups arrived at this conclusion using two distinct processes.
Each person shifted 5 times; 5 × 5 = 25. By changing positions of 5 people until the first one occupies the first position again.
Learner A sits in 5 times
Learner B sits in 5 times
Learner C sits in 5 times
Learner D sits in 5 times
Learner E sits in 5 times
5 + 5 + 5 + 5 + 5 = 25
According to statistics there is only one way 5 people can sit around a circular table. The first person can occupy any of the five positions. The same could happen to the remaining four people. In this manner all five people will occupy 5 different positions, which means 5 people, 5 positions each. We multiply 5 by 5 to obtain 25 (5 × 5 = 25) ways.
Explanation 1 suggests that the learners were counted separately and not in their strings of seating arrangements. Each of the five learners had an opportunity to occupy any of the five seats, translating into a total of 25 possibilities. The potential to scaffold this into the concept of factorial is very low as there are numerous issues (structure, permutations) that need to be addressed.
Explanation 2 deploys an external tool: statistics. The explanation did not make it clear whether all the seats were occupied simultaneously or one at a time.
Reflecting on the students’ challenges in working from practical engagement
The students’ responses to the assigned task reveal two key challenges associated with dealing with mathematical concepts encountered in real-life situations. The first challenge is that students struggle with representing the problem in a way that makes it accessible mathematically. Each group had no problem in realising that they were dealing with a counting activity as reflected in the four conclusions presented. Initially they thought that role-playing the situation would enable them to observe and better understand the given factorial function problem. Lack of systematisation made this option less feasible, leading to its abandonment. Acting out as a form of direct representation proved ineffective as people proved hard to manipulate (as learning aids). This led to the use of letters of alphabet as symbolic representations of people. Letters proved easier to manipulate, as evident in almost all the responses. However, the choice of letters imposed yet another restriction. In all the cases, either the first or the last five subsequent letters were chosen and the order was rigidly adhered to and maintained. The order of taking the first letter to the last resulted in a different seating arrangement only if one deals with linear arrangement. In a circular arrangement, one ends up with the same seating arrangement. The second challenge was the problem of how multiplication manifests itself in real-life situations. In real life, multiplication is encountered as repeated addition of the same quantity. Thus we do not look for multiplication per se but for the same quantity added a number of times.
Textual experiences, interpretations and applications
At this stage, students were given a handout explaining the factorial concept and differences between linear and circular arrangements. Furthermore, they were advised to make use of Internet and library services to find more information. This exposure alerted students to a different way of learning mathematics – the use of literature (Bintz & Moore, 2003) rather than a prescribed textbook. This offered students an opportunity to review their earlier submissions. The second set of students’ written responses followed this intervention. Two different answers were arrived at: 120 and 24 permutations.
Seven groups arrived at 120 seating permutations. Their procedures, interpretations and justifications fall into three different categories.
The first category comprises students who used colours.
Explanation 1: Use of colours to represent the five people.
It is a probability problem, which needs possible outcomes. …We first took 2 people and sit them opposite to each other and not allowing them to change positions. For example we name our 5 people, green, blue, red, yellow and white then sit them such that red is opposite green. Make green and red not moving and let the others change positions. For example:
Red, Green, Blue, White, Yellow
Red, Green, Blue, Yellow, White
Red, Green, Yellow, Blue, White
…
There are six possible arrangements. If we fix the position of red and replace green, we also find another six possibilities. If we continue by not altering the positions of red and changing the ones that sit opposite red, we found 24 outcomes (6 × 4). If we change the position of red and replace it by each of the other colours at a time, we will have another 24 arrangements different to each colour and we multiply the 24 different arrangement by the number of colours we found a total of 120 arrangement (5 × 24).
Initially, the students classified the activity as a probability problem. However, that did not influence what followed. Instead, the students developed a systematic way of representing the different arrangements. The technique involved fixing some positions while exchanging the others. This improved the clarity of their observations and they thus appeared to have extended standard odometer thinking to wacky odometer thinking (Halani, 2013). Ultimately, they arrived at 24 arrangements for each colour occupying the first position resulting in 5 × 24 = 120 different possible combinations. The use of colours resolved the rigidity of linearisation inherent in the use of letters.
The second category comprised students who used the factorial formula without justifying its link to the problem at hand. The distinction between linearity and circularity was not addressed.
Say that people are seated as person A; B; C; D and E. Such an order can be represented in a linear list as ABCDE. With the use of this notation, we can count the number of possible lists. There are:
5 possible choices for the first spot (A, B, C, D or E)
4 choices for the second
3 choices for the third
2 choices for the fourth
1 choice for the fifth spot.
That is, there 5× 4× 3× 2× 1=120 ways. The list can be written as:
ABCDE; ABCED; ABECD; ABDEC; EBDCA; EDBCA; etc. Therefore, there are 120 ways.
The five people keep changing seats one at a time in such a way that none of them repeats to have the same neighbour.
A string of five letters was used as a way of representing people. However, the rigidity of the order of the letters was rescinded. Having explored the possibilities of occupying each of the positions, the group then used multiplication to arrive at 120. The transition from choices for each seat to multiplication is not clear. This transition makes their explanation similar to those in which a formula was used.
The third category comprised explanations that provided some link between representation using letters and factorial function. The students first made use of formulae to calculate the number of permutations, they then use actual seating, represented by letters, to confirm their findings.
5!=5× 4× 3× 2× 1=120
Therefore, there are 120 ways
Since these people are to sit in different ways, this implies repetition is not allowed and the order at which these people are arranged is important. The number of permutations of ׳n׳ different people taken at a time is as follows: First mark the sitting positions as 1; 2; 3; 4; 5. Note that the positions must be at equal distance from each other to avoid conflict. Name the five people as A; B; C; D and E. Sit one person at a time. Since there are five people, the first person, suppose is ‘A’ can sit in 5 ways. The second person ‘B’ from the four remaining can sit in ‘4’ ways as the fifth position is occupied by ‘A’. The third person ‘C’ will sit in 3 ways and the fourth will sit in 2 ways. Finally the fifth person ‘E’ will sit in only one way. …
This can be:
| ABCDE |
ABECD |
ABDCE |
ACEDB |
AEBDC |
| ACDEB |
ACDBE |
ABEDC |
ADBEC |
AECDB |
| ADEBC |
ADBCE |
ACBDE |
ADCBE |
AEDBC |
| AEBCD |
AEBCD |
ACBED |
ADCEB |
AEDCB |
| ABDEC |
ABCED |
ACEBD |
ADECB |
|
This arrangement gives 24 positions if A is fixed in the 1st position. Another 24 when A is fixed in the 2nd position and so on resulting in 24+24+24+24+24=120 ways
There are 120 ways
1!=1
2!=2× 1=2
3!=3× 2× 1=6
4!= 4× 3× 2× 1=24
5!= 5× 4× 3× 2× 1=120
For 5 people we have
5!=5× 4× 3× 2× 1=120
∴ 120 ways
We indicated person number 1 as A; 2 as B; 3 as C; 4 as D and 5 as E
| No. |
1 |
2 |
3 |
4 |
5 |
| 1 |
ABCDE |
BACDE |
CABDE |
DABCE |
EABCD |
| 2 |
ABCED |
BACED |
CABED |
DABEC |
EABDC |
| 3 |
ABDCE |
BADCE |
CADBE |
DACBE |
EACBD |
| ⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
⋮ |
| 24 |
AEDCB |
BEDCA |
CEDBA |
DECBA |
EDCBA |
Each person can sit in 24 ways and there are 5 people.
∴ 24× 5=120
In explanation 3, the permutation strategy is used. The strategy was confirmed by showing what all arrangements that begin with letter A would look like. The point was made by the students that, since there are five different letters, a conclusion of 5 × 24 = 120 makes sense. In explanation 4, the notion of the factorial function is extrapolated from a simple situation to the one where there are five people. This was followed by the actual representation of those ways using letters.
While conclusions are simultaneously drawn from two contexts, the link between those contexts remains obscure. The notion of a factorial as a product of all positive integers equal to and less than the given number is not matched by the representations that students used. Two systems that are not necessarily aligned have now taken hold in students’ engagement with the task.
In this case groups resorted to strong algorithmic procedures where numbers were processed without any justification given for the action taken. In all instances, the first part of the strategy was to calculate the number of possible arrangements, assuming that they were in a linear form. A total of 120 permutations was arrived at. The second part involved division by 5, arguing that the circular arrangement warranted division. The rationale for division by 5 was not explained. However, two different categories could still be observed: (1) abrupt transition without justifying the transition from linear to circular and (2) a fairly appropriate justification that showed only language as a challenge, not the understanding of the concept.
In the first category, students resorted to strict adherence to the formula found in the text. The linear arrangement was used to find the total number of possible outcomes. Division was then used to arrive at the arrangements for a circular setting. A typical response is seen in explanation 1.
Five people have 5 factorials in a linear permutation. The linear permutation is found when multiplying the factorials of five: 5× 4× 3× 2× 1=120. To convert it to circular permutation you have to divide the linear permutation by the number of people, 120÷ 5=24 The formula can be defined as 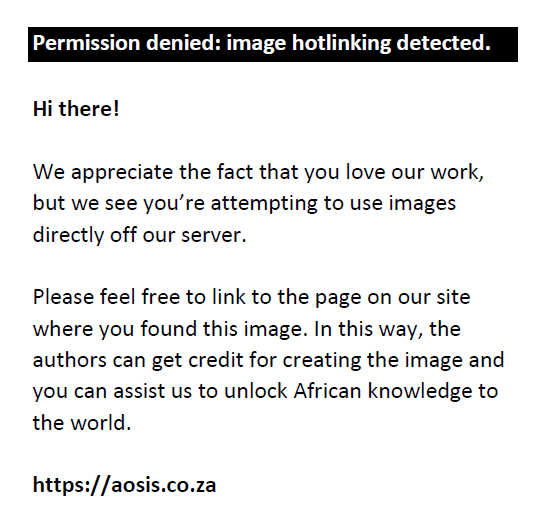
The rationale for division by the number of seats as they convert from the linear to circular permutations was not given. The way the information was presented suggests that the action was undertaken because the formula suggested it.
In the second category, students started the same way as in the first. However, the impact of a circular arrangement on the distinction of these arrangements is recognised and acknowledged.
A round table differs with a normal table in that it has no ends. Therefore, you can arbitrarily select seat #1.
You can fix one person in place (or, equivalently, rotate the table like a carousel so that that person always winds up in the same place). This will avoid multiple equivalent scenarios in which the people are seated in the same order, but have just shuffled a seat or two over (these don’t count as different arrangements). Then you have free rein to arrange the other four people, so that’s 4!=24 arrangements. Alternatively, you can figure out that there are 5!=120 arrangements overall. However, each unique arrangement is actually repeated five times because there are five seats around the table, there are 5 different versions of every possible seating arrangement. (For instance, ABCDE, BCDEA, CDEAB, DEABC, EABCD are all equivalent). So this means you must divide by 5: 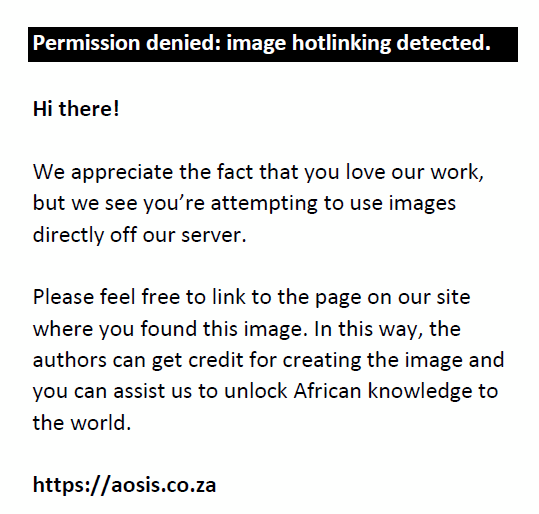 . .
The case for repeating arrangements was adequately made and demonstrated in the response. The conclusion that ‘each different representation is actually represented 5 times’ is critical to the ultimate formula for calculating the circular arrangement. The only uncertainty was the connection between the repeating arrangements and the use of division to address that. Can one say that the students had consciously used the division by 5 to counter the five repetitions? More explanation would have provided a better perspective in this regard. Later on in this article we show how these kinds of gaps translate into challenges when the solutions are to be explained in a pedagogic situation.
Reflecting on textual experiences, interpretations and applications
The students’ engagement with text reveals two insights into their learning, especially in mathematics: the authoritative role that text plays and the gap between real life and mathematical representations.
Authoritative role of text in students’ learning: Upon receiving the text, the students focused on how a number of arrangements could be calculated given the number of objects. Since the text first addressed arrangements in a linear setting and later those in a circular setting, students used exactly the same approach in responding to their assigned task. In particular, the focus was on the formulae given in the text. This appeared to have obstructed their ‘mental flexibility in switching from one solution method to another’ (Amit & Neria, 2008, p. 124). For the majority of students, identification of the formula was an end in itself. We saw this in students who arrived at the response of 120. Immediately after identifying the formula for n! they plugged it in and stopped. Nothing much was done in terms of how well the formula represented the task at hand. The same challenge was observed with those students who arrived at an answer of 24.
While this group could clearly differentiate between linear and circular arrangements, it is the transition between the two that reflects the authoritative power of the text. The formula 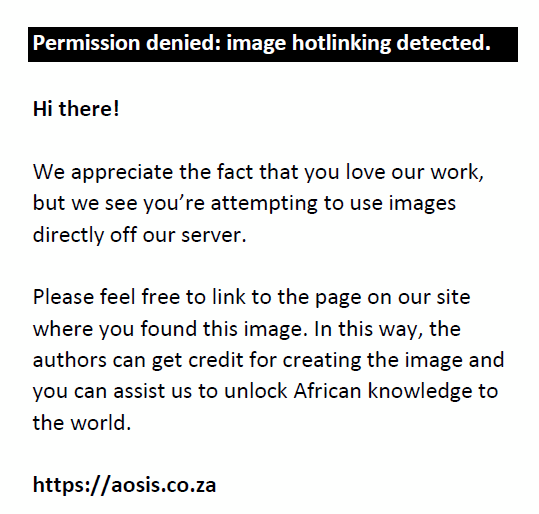 was simply accepted as appropriate for circular arrangements without much effort to justify it. The problem with this approach is that it relinquishes the responsibility for learning to the text and, by implication, to the author. It is the author’s responsibility to explain why a particular idea works and how it works in reality. was simply accepted as appropriate for circular arrangements without much effort to justify it. The problem with this approach is that it relinquishes the responsibility for learning to the text and, by implication, to the author. It is the author’s responsibility to explain why a particular idea works and how it works in reality.
The gap between real life and mathematical representations: How does division manifest itself in the real world and can it be observed? This seems to be a major obstacle in how the students moved from linear to circular arrangements. What is 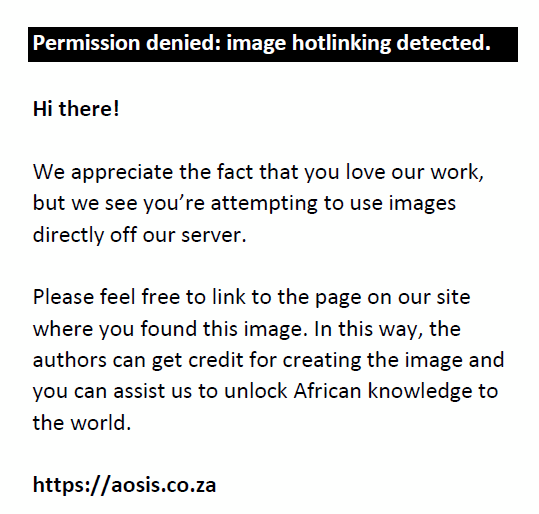 in the real world? Saying the statement is about 120 divided by 5 does not say much more than how the statement reads. However, if one sees 120 divided into fives (groups of 5) or 120 divided into five groups, or repeated subtraction of 5 from 120, then one has more chance of observing the phenomenon in reality. Limited use of varied verbal representations, among other things, denies our students the richness of observing and engaging with mathematical objects in real life. As argued by Elia and Spyrou (2006), mathematics teaching in schools focuses on the use of algebraic representations of functions, thus hindering the application of functions in other representational modes. in the real world? Saying the statement is about 120 divided by 5 does not say much more than how the statement reads. However, if one sees 120 divided into fives (groups of 5) or 120 divided into five groups, or repeated subtraction of 5 from 120, then one has more chance of observing the phenomenon in reality. Limited use of varied verbal representations, among other things, denies our students the richness of observing and engaging with mathematical objects in real life. As argued by Elia and Spyrou (2006), mathematics teaching in schools focuses on the use of algebraic representations of functions, thus hindering the application of functions in other representational modes.
Reflections on both practical and textual experiences in a pedagogical context
This section analyses students’ responses to the question of how they would teach the factorial function to Grade 9 learners. The students were asked to reflect on their own experiences in solving the problem at hand. This new perspective prompted varied responses that (1) gave us insights into the depth and quality of students’ understanding of their solutions and (2) revealed complex nature of pre-service teachers’ learning.
Insights into the depth and quality of students’ understanding of their solutions
The students’ struggles with the problem evolved from managing their observations and making sense of text or seeing connections with real life, to expressing their newly constructed knowledge at a basic level that would make Grade 9 learners understand the problem. Almost all the groups encountered a challenge regarding how to systematically observe and record the different seating arrangements, for example:
We decided to do it practically by sitting in a group of five people whereby we were changing our sitting positions. But along the practical route, we got confused and dropped it.
Our frustration is that we are failing to arrange those five people around the table and how will they circulate on that particular table. We find it difficult to determine whether those five people will exchange their seats or just move from one seat to another because that table is circular.
It is this basic challenge of systematisation that later translated into a bigger problem when students were asked to think about how they would teach the concept to a Grade 9 class. The enactment, as they exchanged seats, was disorderly, making it difficult to keep track of which arrangement had been enacted and which had not. The reflections suggest that, at that stage, the students had limited understanding of the problem. However, the introduction of symbolic representation of people through the use of letters and colours allowed the arrangements to be manipulated on paper. Still, the power of the manipulation on paper was not utilised to understand the actual arrangements in reality. Instead, the students were satisfied to arrive at the required number of arrangements.
The continuous interaction between mathematical and real-life representations plays a pivotal role in deepening knowledge construction. It allows one to value the emerging constructs and its absence often leads to frustrations as is evident in the following reflections:
We were frustrated more when someone had the answer but couldn’t explain to us how it could be done by illustrating practically so, by seating on a circular table and changing our seating positions now and again until we get the suitable answer that we had by using the permutation formula.
My frustration is that I didn’t understand the formula of permutations which I have obtained from Internet because if I use this formula to calculate I get 120 ways but if I try to do it practically it becomes impossible. I don’t understand where the formula comes from and how they derived it.
Knowledge, by its nature, enriches one’s sense of seeing. If new knowledge does not enhance one’s broadened vision then there is a challenge. The students’ discovery of the formula in this instance led to frustration instead of a sigh of relief – the ‘aha’ moment. Their inability to relate the textual and the practical experiences was apparent. Crusius (1991, p. 38), using Gadamer’s fusion of horizon, would regard this as a failure of ‘an event of truth, a revealing-concealing that goes beyond the spontaneous, unscrutinized projections of preunderstanding’.
The problem provides insights into the students’ enculturation (Bishop, 1991) in problem-solving. We argue that the challenges encountered are not necessarily limited to the current task but reflect general challenges the students face in dealing with authentic problems in mathematics. It is more of a skill problem than a knowledge one. The way mathematics is traditionally taught in schools does not encourage the ‘seeing’:
I don’t know why we were multiplying instead of adding. … We didn’t know whether we had to add or multiply, but the formula illustrated that we should multiply but still we were more confused because we could not find a suitable answer.
In real-life situations, multiplication manifests itself as repeated addition of the same quantity. In the students’ eyes it is addition that is observed. How that translates into multiplication frustrated them. In the absence of reciprocal translation skills between the two contexts, concepts could be playing themselves out without students noticing.
Complex nature of pre-service teachers’ learning
Learning for the sake of solving a mathematical problem for oneself is different from learning with the purpose of explaining the concept to others. In a context where that ‘other’ involves learners with varying mathematical needs, the demand becomes one where one has to think of a multiplicity of representations at that elementary level. Learning mathematics for others is aligned to Shulman’s (1986, p. 9) pedagogical content knowledge, which includes ‘the ways of representing and formulating the subject that make it comprehensible to others’. For this to happen one must be fairly grounded in the concept.
The students’ reflections in explaining how they would teach factorial function to Grade 9 learners revealed varying degrees of discomfort with their own understanding. From the first set of reflections it was clear that their understanding of the concept lacked depth, for example:
We could not find a suitable answer and we would not know how to explain it to Grade 9s as we don’t know how to explain it between each other.
We were not happy the time when we were not able to find the solution … and we were still confused on what to … teach to Grade 9 learners. It was difficult to reach the answer because we were applying many ways in fact it was really confusing.
With pre-service teacher’s learning, it is important not just to find a solution, but to explain it to oneself or peers, even before thinking of explaining it to others. While in two instances it was obvious that students still had to attend to their own needs, in the next set of reflections it became evident that resolving the problem at their own level was not enough, for example:
We used the formula which is n!. Then we used our calculators to find the answer which is 120. We then tried to make it easy to a Grade 9 learner to understand it. After we had submitted our assignment, the lecturer gave us pamphlets that explain permutation better and they made us to understand better than before. But still the challenge was how we are going to teach that to the Grade 9 learners.
Initially, students went about the task using their own shallow understanding of the problem. The latter part of their reflections was more revealing. The pamphlets helped them understand the problem better than before. However, the challenge of teaching Grade 9 learners became more evident. This means that, while the students were now in a position to deal with the problem at their own level, they could not visualise how the same could be done at a lower level.
In this article we pursued first-year university students’ thinking in solving a real-world problem in a context of minimal teacher interference. Students were exposed to three interactive phases, namely practical experience, textual experience and reflection-on-teaching experience. During practical experience, which Braithwaite and Goldstone (2013) call grounded representations, students were offered an opportunity to see more, to independently manipulate, interpret, reflect in and on action, and to construct visual representations of the problem at hand. During textual experiences, called formal representations by Braithwaite and Goldstone, they engaged with new symbols, calculations and representations. During reflection-on-teaching experience the students were forced to rethink what their new knowledge meant at a conceptually lower level. Drawing from these three interactive phases, we organise our conclusion guided by our research questions.
Challenges associated with engaging in a self-directed learning activity
All the groups experienced varying needs for systematisation in engaging with the problem at hand. This is in line with the findings of English (2005) and Melusova and Sunderlík (2014). Having failed to act out different seating arrangements, symbols were employed, resulting in improved representations. The inherent order of the symbols unfortunately added limitations to representing different arrangements. While manipulatives do facilitate learning (Abramovich & Pieper, 1995), we observed that their inherent features sometimes limit their benefits.
The nature of prior learning also plays a significant role in engaging with combinatorics thinking (Lockwood, 2011; Melusova & Vidermanov, 2015) and we have similar findings. While in real life the students could observe that they were expected to add, the textual experience was encountered in the form of multiplication and division. The two experiential domains could not be reconciled. The students’ prior learning of multiplication and addition was not always reconciliatory especially in the context of real-life experience. We thus conclude that the nature of prior learning, its richness with respect to its representations, is necessary in learning new and unfamiliar mathematics concepts. In this way prior learning facilitates folding back (Pirie & Kieren, 1994).
All the responses, no matter how inconceivable they might have been, offered opportunities for construction of the concept of a factorial function. The mathematical representations used, the struggles with counting different seating arrangements and so on gave us primitive forms of the concept to work with. That is, no matter how unfamiliar the concept is, there is always an opportunity to find a possible baseline to work from, especially when a real-life experience forms part of the engagement.
Ways in which pedagogical attributes affect learning
The question that asked students to reflect on how they would teach the factorial function to Grade 9 learners evoked different orientations to those they used when engaging with the problem. The solutions that were considered adequate no longer held when subjected to the intensity of rethinking them in the context of Grade 9 learners’ capacity to learn. Eventually, it is the viability of their newly found knowledge that is questioned. We observed that the textual experience allowed the students to adopt a formal representation of the factorial function without establishing images of the concept as it manifests itself in the experiential practical world. The knowledge that learners need seems to reside in this gap and the students have limited access to it. Knowledge for teaching requires co-evolution along with content knowledge. It is hard to learn mathematics content first and only thereafter think of how to teach that content at lower levels, or at the same level for that matter. The rich, meaningful and conscious evolution of concept formation allows students multiple perspectives from which they can engage with learners at various stages of learning. Any struggle a student encounters in figuring out how to help learners learn a particular concept is a sign that there are gaps in the student’s learning of the concept itself.
Mathematics content knowledge that is approached from a pedagogical context is process-rich and multi-representational, and so poised to serve learning of new and unfamiliar concepts. In this orientation, pre-service teachers’ learning is more engaging than is traditional mainstream mathematics content learning. Melusova and Sunderlík (2014) arrived at the same conclusion when they investigated pre-service teachers’ problem-solving processes in combinatorics. We observed that when the students had to solve the problem for themselves, they hurried through some aspects of their learning, focusing more on the actual solution. They were more product-driven than process-focused. That way, learning outcomes were limited in their usefulness. We are, therefore, persuaded that pedagogical attributes, when meaningfully incorporated into the learning of new and unfamiliar mathematics concepts, enrich learning and orient knowledge to productively service future learning.
Competing interests
The authors declare that they have no financial or personal relationships that may have inappropriately influenced them in writing this article.
Authors’ contributions
S.M. (University of Limpopo) was the project leader, facilitated the lessons and therefore engaged in initial data collection. Reflections on students’ submissions, data analysis and write-up were done by both S.M. and K.M. (University of Limpopo).
Abramovich, S., & Pieper, A. (1995). Fostering recursive thinking in combinatorics through the use of manipulatives and computing technology. The Mathematics Educator, 7(1), 4–12.
Amit, M., & Neria, D. (2008). “Rising to the challenge”: Using generalization in pattern problems to unearth the algebraic skills of talented pre-algebra students. ZDM: The International Journal on Mathematics Education, 40(1), 111–129. http://dx.doi.org/10.1007/s11858-007-0069-5
Bhargava, M. (2000). The factorial function and generalizations. The American Mathematical Monthly, 107(9), 783–799.
Bintz, W.P., & Moore, S.D. (2003). Using literature to teach factorials. Mathematics Teaching in the Middle School, 8(9), 461–465.
Bishop, A. (1991). Mathematical enculturation: A cultural perspective on mathematics education. Dordrecht: Kluwer Academic Publishers. http://dx.doi.org/10.1007/978-94-009-2657-8
Bitsch, V. (2005). Qualitative research: A grounded theory example and evaluation criteria. Journal of Agribusiness, 23(1), 75–91.
Braithwaite, D.W., & Goldstone, R.L. (2013). Integrating formal and grounded representations in combinatorics learning. Journal of Educational Psychology, 105(3), 666–682.
Charmaz, K. (2008). Grounded theory as an emergent method. In S.N. Hesse-Biber, & P. Leavy (Eds.), Handbook of emergent methods (pp. 155–172). New York, NY: The Guilford Press.
Creswell, J.W. (2007). Qualitative inquiry and research design: Choosing among five approaches. (2nd edn.). Thousand Oaks, CA: Sage Publications, Inc.
Crusius, T.W. (1991). A teacher’s introduction to philosophical hermeneutics. Urbana, IL: National Council of Teachers of English.
Elia, I., & Spyrou, P. (2006). How students conceive function: A triarchic conceptual-semiotic model of the understanding of a complex concept. The Montana Mathematics Enthusiast, 3(2), 256–272.
English, L. (2005). Combinatorics and the children’s development of combinatorial reasoning. In G.A. Jones (Ed.), Exploring probability in schools: Challenges for teaching and learning (pp. 121–144). New York, NY: Springer.
Erickson, F. (1998). Qualitative research methods for science education. In B.F. Fraser, & K.G. Tobin (Eds.), International handbook of science education (pp. 1155–1173). Dordrecht: Kluwer Academic Publishers.
Glaser, B.G., & Strauss, A.L. (1967). The discovery of grounded theory. Chicago, IL: Aldine.
Guba, E.G., & Lincoln, Y.S. (1989). Fourth generation evaluation. Newbury Park, CA: Sage Publications.
Halani, A. (2013). Students’ ways of thinking about combinatorics solution sets. Unpublished doctoral dissertation. School of Mathematical and Statistical Sciences, Arizona State University, Tempe, Arizona, USA. Available from http://hdl.handle.net/2286/
Lockwood, E.N. (2011). Student approaches to combinatorial enumeration: The role of set-oriented thinking. Unpublished doctoral dissertation. Portland State University, Portland, Oregon, USA. Available from http://pdxscholar.library.pdx.edu/cgi/viewcontent.cgi?article=1337&context=open_access_etds
Malisani, E., & Spagnolo, F. (2009). From arithmetic thought to algebraic thought: The role of the “variable”. Educational Studies in Mathematics, 71, 19–41.
Maoto, S., & Wallace, J. (2006). What does it mean to teach mathematics for understanding? When to tell and when to listen? African Journal of Research in Mathematics, Science and Technology Education, 10(1), 59–70.
Melusova, J., & Sunderlík, J. (2014). Pre-service teachers’ problem posing in combinatorics. In O. Šedivý, V. Švecová, D. Vallo, & K. Vidermanová (Eds.), Proceedings of the 12th Mathematical Conference in Nitra (pp. 115–122). Available from http://www.nmk.fpv.ukf.sk/2014/
Melusova, J., & Vidermanov, K. (2015). Upper-secondary students’ strategies for solving combinatorial problems. Procedia - Social and Behavioral Sciences, 197, 1703–1709.
Pirie, S., & Kieren, T. (1994). Growth in mathematical understanding: How can we characterise it and how can we represent it? Educational Studies in Mathematics, 26(2), 165–190. http://dx.doi.org/10.1007/BF01273662
Schön, D.A. (1983). The reflective practitioner. New York, NY: Basic Books.
Shulman, L.S. (1986). Those who understand: Knowledge growth in teaching. Educational Researcher, 15(2), 4–14.
Skemp, R.R. (1978). Relational understanding and instrumental understanding. The Arithmetic Teacher, 26(3), 9–15.
Tall, D. (2008). The transition to formal thinking in mathematics. Mathematics Education Research Journal, 20(2), 5–24.
Tarlow, L.D. (2008). Sense-able combinatorics: Students’ use of personal representations. Mathematics Teaching in the Middle School, 13, 484–489.
Tobin, K., & Tippins, D. (1993). Constructivism as a referent for teaching and learning. In K. Tobin (Ed.), The practice of constructivism in science education (pp. 3–21). Hillsdale, NY: Lawrence Erlbaum Associates.
Vygotsky, L.S. (1962). Thought and language. Cambridge, MA: MIT Press.
|