Abstract
The ability to reason about numbers in relative terms is essential for quantitative literacy, which is necessary for studying academic disciplines and for critical citizenship. However, the ability to reason with proportions is known to be difficult to learn and to take a long time to develop. To determine how well higher education applicants can reason with proportions, questions requiring proportional reasoning were included in one version of the National Benchmark Test as unscored items. This version of the National Benchmark Test was taken in June 2014 by 5 444 learners countrywide who were intending to apply to higher education institutions. The multiple choice questions varied in terms of the structure of the problem, the context in which they were situated and complexity of the numbers, but all involved only positive whole numbers. The percentage of candidates who answered any particular question correctly varied from 25% to 82%. Problem context and structure affected the performance, as expected. In addition, problems in which the answer was presented as a mathematical expression, or as a sentence in which the reasoning about the relative sizes of fractions was explained, were generally found to be the most difficult. The performance on those questions in which the answer was a number or a category (chosen as a result of reasoning about the relative sizes of fractions) was better. These results indicate that in learning about ratio and proportion there should be a focus on reasoning in various contexts and not only on calculating answers algorithmically.
Introduction
One valued attribute of a university graduate is a degree of quantitative literacy appropriate to their discipline. This means that graduates should be able to engage confidently with data in an informed and critical way. However, many programmes of study expect students to have this ability as undergraduates. For example, as seen in Social Sciences and Health Sciences contexts, progress made in addressing challenges facing society can be examined by means of measuring change in statistical indicators such as poverty rates, government spending on social grants, infection rates and lifestyle risks. Meaningful comparison of the values of indicators at different times, or between different indicators, usually entails consideration of both absolute and relative quantities, that is, reasoning with proportions is necessary. Reasoning with proportions is clearly also an essential ability in scientific disciplines.
Thus it is important for students to be able to reason logically and confidently with relative quantities and furthermore to be able to explain this reasoning. From our experience of teaching quantitative literacy to university students, we have observed that proportional reasoning is a troublesome concept; it is difficult to learn and takes a long time to learn. Consequently, we regard proportional reasoning as a ‘threshold concept’ (Meyer & Land, 2003) for all academic quantitative literacy (Frith & Lloyd, 2014; Lloyd & Frith, 2013). This threshold concept, once mastered, opens a gateway to thinking differently about quantities.
Although solving problems involving ratio and proportion is part of the curriculum for both Mathematics (Department of Basic Education, 2011a) and Mathematical Literacy (Department of Basic Education, 2011b) in primary and high school, it is useful to know to what extent students are able to reason with proportions when they enter higher education. This information is also useful for school teachers whose goal it is to ensure that learners are adequately prepared for tertiary education as well as for critical citizenship.
In this article we discuss the results of an assessment of the proportional reasoning ability of learners who aspire to enter higher education institutions and who wrote the Academic and Quantitative Literacy component of the National Benchmarks Tests (NBT). This is mainly intended to inform both school teachers and university lecturers about the general ability of these learners to reason with proportions. It also highlights some of the factors that affect the difficulty of this kind of reasoning.
The nature of quantitative literacy and proportional reasoning
In the literature there are many different definitions of quantitative literacy (or numeracy), which is the same competency that is embodied in the school subject Mathematical Literacy (Department of Basic Education, 2011b). Different definitions emphasise different aspects of this complex concept, but the idea that it is mainly concerned with mathematics and statistics used in context is essential to all of them (e.g. Chapman & Lee, 1990; Jablonka, 2003; Johnston, 2007; Steen, 2004). In this study we use the following definition:
Quantitative literacy (numeracy) is the ability to manage situations or solve problems in practice, and involves responding to quantitative (mathematical and statistical) information that may be presented verbally, graphically, in tabular or symbolic form; it requires the activation of a range of enabling knowledge, behaviours and processes and it can be observed when it is expressed in the form of a communication, in written, oral or visual mode. (Frith & Prince, 2006, p. 30)
The formulation of this definition is strongly influenced by the definition of numerate behaviour underlying the assessment of numeracy in the Adult Literacy and Lifeskills Survey (Gal, Van Groenestijn, Manly, Schmitt & Tout, 2005) and the view of academic literacy and numeracy as social practice. In this definition, the ‘range of enabling knowledge, behaviours and processes’ refers to the competences necessary for quantitative literacy practice, which include number sense, some basic mathematical abilities and quantitative reasoning in context. One of the most crucial competences, in our view, is that of proportional reasoning, that is, reasoning with numbers in relative, not absolute terms.
According to Lamon (2007), in her review of research on proportional reasoning and rational numbers, the term ‘proportional reasoning’ has become an ill-defined term ‘referring to anything and everything related to ratio and proportion’ (p. 637). However, she pointed out that the research on ratio and proportion has implicitly defined proportional reasoning in terms of two problem types, ‘comparison problems’ and ‘missing value problems’. In a comparison problem two ratios  and and  are given and it must be determined which is larger or whether they are equal. Missing value problems are ones where three of the four values in a proportion are given and it must be determined which is larger or whether they are equal. Missing value problems are ones where three of the four values in a proportion  are given and then the fourth value must be found. are given and then the fourth value must be found.
A broader definition for proportional reasoning was proposed by Lamon (2007, p. 638):
Supplying reasons in support of claims made about the structural relationships among four quantities, (say a, b, c, d) in a context simultaneously involving covariance of quantities and invariance of ratios or products; this would consist of the ability to discern a multiplicative relationship between two quantities as well as the ability to extend the same relationship to other pairs of quantities.
She stressed the need to supply reasons because many students can provide a correct numerical answer to a proportion problem using an algorithmic procedure, but this does not necessarily mean that they actually employed proportional reasoning.
Research on proportional reasoning
In the middle of the last century Piaget’s theory established proportional reasoning as a defining characteristic of the formal operations stage of development of thinking (Inhelder & Piaget, 1958). As a consequence, research into the development of proportional reasoning of children and adolescents has been carried out and has continued since then. Tourniaire and Pulos (1985), in their review of the literature of the previous 25 years, claimed that the existing research was disjointed and difficult to apply to mathematics education. The Rational Number Project in the late 1980s and early 1990s produced numerous articles on proportional reasoning (e.g. Cramer, Post & Currier, 1993; Harel, Behr, Post & Lesh, 1991; Lesh, Post & Behr, 1988). When Lamon (2007) reviewed the research on the topic she noted that there was only a small number of researchers engaged in long-term research agendas in the field at that time. However, the research mentioned above all points to the fact that
fractions, ratios and proportions are the most protracted in terms of development, the most difficult to teach, the most mathematically complex, the most cognitively challenging, the most essential to success in higher mathematics and science. (Lamon, 2007, p. 629)
Tourniaire and Pulos (1985) summarised the research done on the difficulties that children and adults have in reasoning with fractions, proportions and ratios and concluded:
Despite its importance in everyday situations, in the sciences and in the educational system, the concept of proportions is difficult. It is acquired late. … Moreover, many adults do not exhibit mastery of the concept. (p. 181)
They also claimed that we could expect the majority of learners to be able to successfully solve proportion problems only in late adolescence. Lamon (2007, p. 637), even more dramatically, said that her ‘own estimate is that more than 90% of adults do not reason proportionally’. She went on to say that ‘many adults, including middle school teachers … and preservice teachers … struggle with the same concepts and hold the same primitive ideas and misconceptions as students do’ (Lamon, 2007, p. 633). Courtney-Clarke and Wessels (2014) found that only 25% of preservice teachers in a study in Namibia could recognise the relative size of two common fractions in a comparison problem.
One might assume, however, that the fraction of people who can reason proportionally would be greater within prospective higher education students than in the general population, but ‘proportional reasoning remains problematic for many college students’ (Lawton, 1993, p. 460). In a study at US colleges, Thornton and Fuller (1981) found that only about 75% of science students had a sound grasp of the ratio concept and Lawton (1993) found that only about half of the psychology students she studied could solve simple proportion problems. A recent South African study (Harries & Botha, 2013) of third-year medical students’ ability to perform dosage calculations involving proportions found that only 23% were able to do these correctly.
Clearly it is therefore necessary to make more sustained efforts to teach proportional reasoning at both school and higher education levels. Lamon (2007) however pointed out that there are no quick fixes for students who have not developed a proportional reasoning ability appropriate to their stage of development. Short-term teaching interventions ‘have been largely ineffective’ and ‘indicate that building fraction, ratio and proportion knowledge will involve a long-term learning process’ (Lamon, 2007, p. 645).
Another very important observation made by Lamon (2007) is that reasoning intuitively about proportions can be made more difficult for students by their having learned algorithmic methods in mathematics classes. She reported that young children have been shown to have quite powerful intuitive reasoning strategies, but that a few years of mathematics instruction weakens this ability and replaces it with rules and algorithms that are frequently applied incorrectly. This results in challenges in teaching for understanding.
Factors affecting the difficulty of proportional reasoning problems
Tourniaire and Pulos (1985) and Lamon (2007) reviewed the numerous studies of factors that influence the difficulty of proportional reasoning problems. An obvious factor affecting difficulty of problems is the size and type of numbers to be worked with. However, recognising this difficulty, researchers have often used easy numbers (less than 30) and integral ratios in their studies in order to avoid the interaction effect of difficult numbers (Heller, Post & Behr, 1985).
Among the many other factors that have been studied are those of context and structure of the problems to be solved. The context of a task includes the event in which the task is situated and the language used to describe both task and event (Van Den Heuvel-Panhuizen, 2005). Included in this notion of context are issues such as whether the measures used in the problem are discrete or continuous, whether the context of the problem involves mixtures (such as dilutions) and whether the event is familiar. Tourniaire and Pulos (1985) suggested that problem-solving strategies used by students in solving mixture and non-mixture problems are different and that discrete quantities in mixture problems are more easily visualised. Lawton (1993) concluded that college students are more likely to use proportional reasoning when the measures used in a mixture problem are discrete.
Bell, Fischbein and Greer (1984) found that familiarity with the context is important, as seen in the competent handling of price stories by 12- and 13-year-olds. Heller et al. (1985) concluded that Grade 7 students found the less familiar context of petrol consumption more difficult than that of speed. Tourniaire and Pulos (1985) agreed that familiarity with the context makes problems easier to solve, but only if the student is also familiar with using ratios in that context.
Bell et al.’s (1984) work on problem structure confirmed the known misconceptions about multiplication and division rate problems, such as that multiplication always makes bigger and division always makes smaller. They reported that division of a smaller number by a bigger one often leads to reversals of operations by students. In rate problems requiring division, the easiest to solve are those that are of the partition type (e.g.  , where the distance can conceivably be partitioned into as many subsets as there are time units). Problems in which the divisor is itself a rate (e.g. , where the distance can conceivably be partitioned into as many subsets as there are time units). Problems in which the divisor is itself a rate (e.g.  ), which are of the quotition type, are more difficult. ), which are of the quotition type, are more difficult.
In a small study of preservice elementary teachers, Conner, Harel and Behr (1988) looked at the effect of two structural variables on the level of difficulty of missing value problems, namely the position of the missing value and the coordination of the measure spaces as stated in the question. The measure spaces contain the variables being considered in the question and they are coordinated when the variables are mentioned in the same sequence within the two statements making up the question. For example, the measure spaces (apples and cost) are coordinated in the question ‘If 5 apples cost R6, 8 apples cost how much?’ whereas in the question ‘If 5 apples cost R6, what will be the cost of 8 apples?’ they are not coordinated. The two statements making up the question can also be rearranged so that the open statement (containing only one value) comes before the closed statement (containing two values), for example ‘what will be the cost of 8 apples if 5 apples cost R6?’ The results of the study indicated that the coordination of measure spaces did not pose as much of a problem as did the position of the missing value within the open statement, as they hypothesised that students are able to transform the structure of the problem by changing the order of the quantities in the open statement so that the measure spaces are coordinated. However, in follow-up research Harel and Behr (1989) suggested that there may be differences in the strategies used in such problem-structure transformations by high performers and low performers.
The results reported in this article highlight the effect of two factors affecting proportional problem difficulty that have been described above, namely context and problem structure.
Method
Ethical clearance for this project was obtained from our Faculty Research Ethics Committee in a process that included the approval of the consent form that is signed by all candidates of the NBT, allowing the use of their results for research purposes.
Before we describe the questions used in this research to investigate prospective students’ proportional reasoning, we need to clarify our terminology. There is some debate about the meanings of the terms ‘ratio’, ‘rate’, ‘fraction’ and ‘proportion’ (Lamon, 2007), but in describing the structure of the questions, we will use only the terms ‘rate’ or ‘fraction’ to refer to any number in the form  , where a and b can be any numbers or measurements (with b ≠ 0 ). A rate or fraction may be represented as a decimal fraction, a percentage or in some other conventional way. Some examples are speed, cost per item, birth rate (births per 1 000 of the population) and crime rate (crimes per 100 000 of the population). , where a and b can be any numbers or measurements (with b ≠ 0 ). A rate or fraction may be represented as a decimal fraction, a percentage or in some other conventional way. Some examples are speed, cost per item, birth rate (births per 1 000 of the population) and crime rate (crimes per 100 000 of the population).
In order to study learners’ proportional reasoning, we mainly used questions that did not require calculation, but reasoning based on an understanding of the way that changes in the values of numerator and denominator will affect the overall value of a fraction (or rate). We were not focusing narrowly on learners’ ability to work algorithmically with the concept of proportion, but on their reasoning; thus, only two of the nine questions required an answer to be calculated. In order to avoid the numerical difficulty effect, the numbers used in the questions were positive integers and mostly small in size; any large numbers used were simple multiples of powers of 10. These questions are examples of problems of both missing value and comparison types, but in some cases the latter are more complex than determining only the order of two fractions, requiring the values of denominators to be compared. These are examples of what Harel et al. (1991, p. 127) described as ‘advanced multiplicative reasoning in which ratios and products are compared in terms of changes and compensations’.
The questions were administered as part of the NBT Academic Literacy Test, which includes assessment of quantitative literacy. The questions were multiple choice items with four alternative answers. The version of the test that included these items was written by 5 444 candidates in June 2014 and the alternative chosen by each candidate for each question was recorded. The questions were interspersed among trial items placed at the end of the test and did not contribute to candidates’ scores.
The first three questions used in this study were missing value questions and had the same mathematical structure, being of the form: ‘If A is equivalent to B, then C is equivalent to what?’, where quantities A, B and C are given and the context is clearly one of direct proportion. The simplicity of the numbers and the familiarity of the contexts differed between questions. Question 1 and Question 2 were simple calculations in a familiar and less familiar context respectively, while Question 3 required candidates to recognise the answer in the form of a mathematical expression, rather than to calculate it. In this case the context was also less familiar and the numbers did not divide easily.
Question 4, Question 5 and Question 6 were comparison type questions in which the numerator and denominator of four rates were given and candidates had to identify the rate with the biggest value. In Question 6 they had to identify the largest of four common fractions. Question 4 and Question 5 were presented in a similar way, using the context of speed and TB infection rates (cases per 1 000 of the population) respectively. Question 4 is reproduced below to illustrate how these questions were presented:
The table summarises the distance travelled and the time taken by four different cars. Which car drove at the fastest speed?
|
Car A |
Car B |
Car C |
Car D |
| Distance (km) |
110 |
110 |
100 |
100 |
| Time (minutes) |
40 |
60 |
60 |
40 |
(A) Car A (B) Car B (C) Car C (D) Car D
Question 7 and Question 8 were presented in the same way as Question 4 and Question 5 and used the same or very similar contexts. However, for these questions the problem was not to compare the values of the rates, but to compare the values of the denominators (that is, time and population respectively).
Table 1 provides a summary of the relevant characteristics of these questions.
| TABLE 1: Summary of the characteristics of the proportional reasoning questions. |
The performance of the candidates on each of the above questions was described by determining the proportions who selected each alternative answer. These proportions were calculated for all candidates and then separately for the candidates in each of four performance bands. The performance bands were determined using the quartiles of the total scores for the 50 scored items in the version of the NBT quantitative literacy test (in which the research items were included as unscored items). So, for example, a candidate was classified as being in the highest quarter if their overall score for those 50 items was equal to or above the third quartile of all the overall scores and a candidate was in the lowest quarter if their overall result was less than or equal to the first quartile.
Results and discussion
The percentages of all candidates selecting the different alternative answers for each question are listed in Table 2. For each question, the percentage selecting the correct answer is given in bold.
| TABLE 2: Percentages of candidates (N = 5 444) who selected the different alternative answers to questions. Correct answers in bold type. |
Missing value problems
Question 1 was a straightforward, simply stated missing value problem (with uncoordinated measure spaces) using easily divisible small whole numbers and the familiar context of the cost of a number of items.
If 4 items cost R5, how much will it cost to buy 20 items?
(A) R1 (B) R16 (C) R20 (D) R25
We expected that all candidates would be able to solve this, probably intuitively, without consciously applying a learned procedure. However, nearly 20% of them did not solve it correctly and 13% chose the answer R20. In Figure 1 it can be seen that, in fact, more than 20% of candidates in the lowest quarter chose this particular incorrect answer (alternative C). In total, nearly 30% of the candidates in the lowest quarter did not solve the problem correctly, which is a far higher proportion than the 6% of candidates in the highest quarter who answered incorrectly. This perhaps indicates a greater ability of the higher performers to transform the problem structure of uncoordinated measure spaces in order to facilitate reasoning, as suggested by Harel and Behr (1989). However, it appears that all candidates who answered incorrectly did not examine their answer critically in the context to see if it made sense.
 |
FIGURE 1: Results for missing value, by performance band. |
|
Question 2 had the same mathematical structure as Question 1, but used the less familiar context of the South African birth rate (expressed as number of births per 1 000 people) with the missing value being the population size. Using this context also meant that the language would be less familiar and that larger numbers were used. However, these were still easily divisible whole numbers. Also, due to the less familiar context the problem statement and presentation of data required three short sentences, thus increasing the language demands of the question. However, unlike the situation in Question 1, the measure spaces were coordinated. From Table 1 we see that only 61% answered correctly and that nearly 20% chose option D, which was an absurdly large number (80 000 000) for the population of a typical South African city, once again revealing that these candidates did not examine their answer critically in the light of the context. Thus, the more complex and less familiar context affected candidates’ performance negatively, even though the problem was structurally the same and the measure spaces in this case were coordinated so that no transformation of the problem structure was required. In Figure 1 it is clear that the negative effect of the change of context (and the associated complexity of the language and size of the numbers) on the performance of the candidates in the lower performance bands is greater than for those in the upper bands.
Question 3 was the same as Question 1 and Question 2 in terms of mathematical structure and, as for Question 1, the measure spaces were uncoordinated:
You need 50 g of a chemical to do 4 repetitions of an experiment. Which of the following is the calculation for finding how many repetitions you can do if you have 125 g of the chemical available?
(A)  (B) (B) 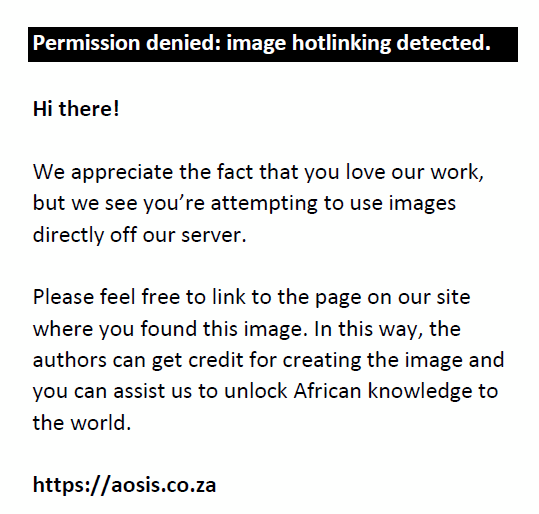 (C) (C) 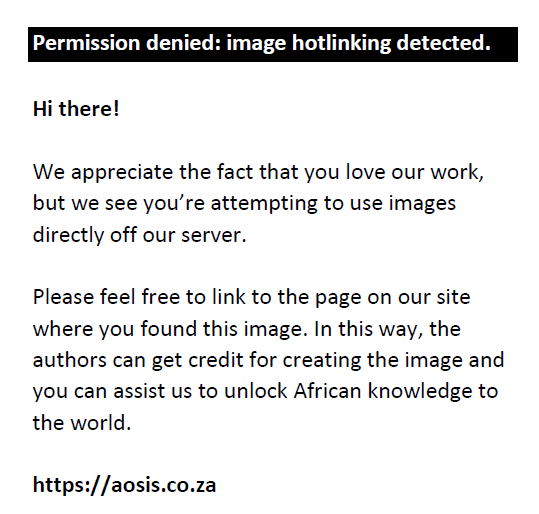 (D) (D) 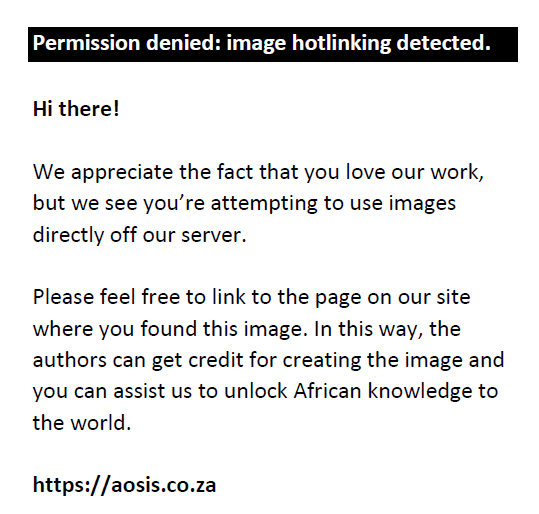
This question used a less familiar context and numbers that were simple whole numbers, but not divisible by each other. The most significant difference between this question and the previous two was that the alternative answers were in the form of fractional expressions representing the calculation of the answer, not the numerical answer itself.
Compared to Question 1, less than half as many candidates could answer this correctly (only 38% of them). Though many could do the calculation in Question 1, the majority could not express the multiplicative procedure for a very similar calculation in the form of an expression (although some of the difference in performance can presumably be ascribed to the less familiar context and more complicated language of the question). This inability to recognise the symbolic representation of the relationships between the quantities involved is consistent with observations made by Bell et al. (1984) in their study of young adolescents. Nearly one-quarter of all candidates chose alternative A, which represents the product of the first two numbers given in the question, divided by the third. Figure 1 shows that in the lower performance bands the percentage who chose option A was greater than the percentage who chose the correct answer. It appears that many of these writers may have been misapplying some learned method, without understanding the meaning of the problem.
Comparison problems (comparing rates)
Question 4, shown earlier in the ‘Method’ section, was a simple problem requiring the comparison of rates in the context of speed, distance and time. Four combinations of distance and time were given and the problem was to identify which represented the greatest speed. The numbers involved were simple, but not divisible by each other, making it necessary to solve the problem by reasoning that the fastest speed resulted from the greatest distance covered in the least time. From Table 1 it can be seen that just under 80% of the candidates could do this correctly, but it is notable that over 10% chose an answer (alternative D) that represented the smallest distance covered in the shortest time. The relatively good performance on this question probably results from the familiar context that most candidates would have experienced in their daily lives. This question provides an example of a partition rate problem, which is considered to be easier than a quotition rate problem (Bell et al., 1984).
Question 5 was identical in terms of mathematical structure to Question 4, but situated in the less familiar context of number of TB cases per 1 000 of the population and requiring four short sentences to state the problem, which was presented as follows:
The infection rate for TB is expressed in terms of ‘cases per 1 000 of the population’. This means that to find the rate the number of cases is divided by the population. The below information summarises the number of cases and the size of the population (number of people) for four communities. Which community had the biggest infection rate?
|
Community A |
Community B |
Community C |
Community D |
| Number of TB infections |
10 |
11 |
10 |
11 |
| Number of people in the community |
1000 |
1000 |
900 |
900 |
(A) Community A (B) Community B (C) Community C (D) Community D
Once again the change to a perhaps less familiar and more complex and reading-intensive context that does not easily allow for intuitive reasoning has resulted in a decrease in the proportion answering correctly (64.8%). Part of the complexity of the context in Question 5 is that, in calculating the rate, a smaller number is divided by a bigger one and this could lead to a reversal of operations, as described by Bell et al. (1984). As was the case for the missing value problems (Question 1 and Question 2), the change of context has adversely affected the candidates in the lower performance bands and hardly affected those in the highest quarter (compare the charts for Question 4 and Question 5 in Figure 2).
 |
FIGURE 2: Results for comparison problems requiring the comparison of the rates, by performance band. |
|
Question 6 was context-free and required candidates to identify the largest of four fractions as follows:
Which of the following is the biggest number? (Do not do any calculations.)
(A) 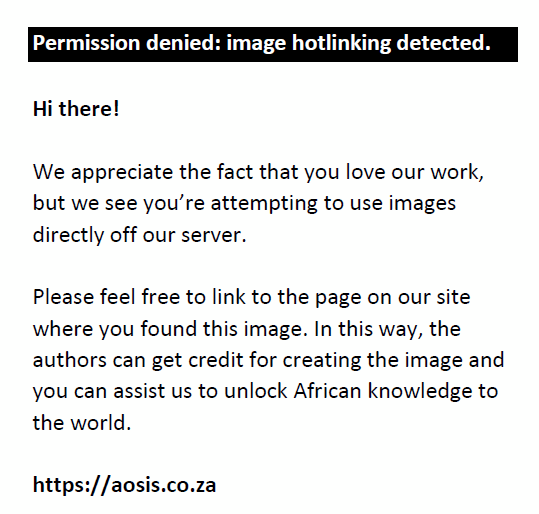 (B) (B) 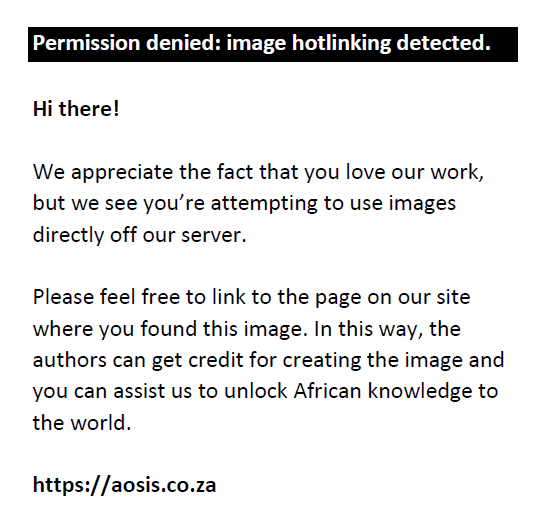 (C) (C) 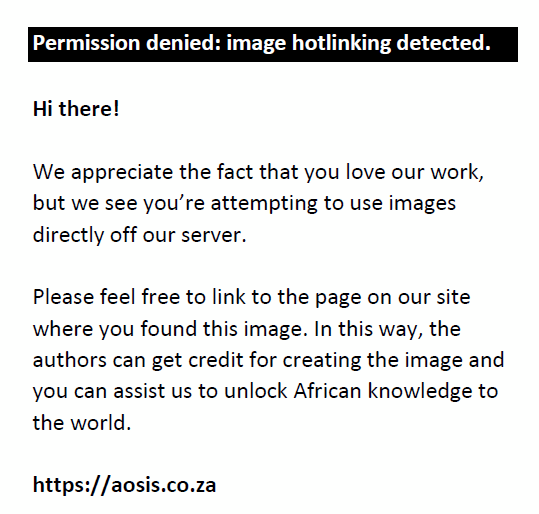 (D) (D) 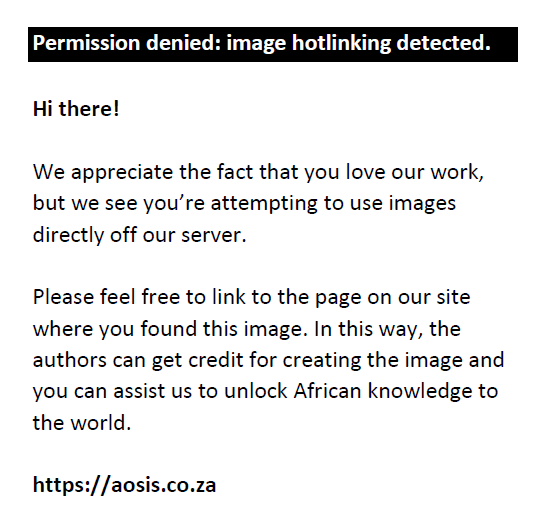
This question has the same mathematical structure as Question 4 and Question 5, but the answers are given as a symbolic mathematical representation. As was the case for Question 3, where the calculation for a missing value question was given in the form of an expression, this fractional representation appears to have made the problem more difficult, though not for the candidates in the highest quarter (see Figure 2). Only 58% of all candidates could identify the largest fraction. This means that 4 in every 10 candidates aspiring to higher education do not appreciate that a smaller denominator and a larger numerator will produce a larger fraction. Almost a quarter of candidates chose alternative A, which had the smallest numerator and the smallest denominator, and 10% chose the fraction with the largest numerator and denominator. The performance was considerably worse in this context-free question, which required applying an understanding of the mathematical concept of fractions, than in both Question 4 and Question 5, where the problem was presented in a context. Even though a more complex context is seen to make a problem more difficult, it still appears that the presence of a context facilitates the reasoning.
For both missing value problems (Question 1, Question 2 and Question 3) and comparison problems (Question 4, Question 5 and Question 6), there is a similar pattern of decreasing performance overall (see Table 1) and similar differences between performance bands (see Figure 1 and the first three charts in Figure 2). So, as the contexts of the problems become increasingly complex, and when alternative answers are given as mathematical expressions, there is a decrease in performance.
Question 7 was also a comparison problem, and similar to Question 6, but somewhat different in that the data was given in the form of a bar chart with stacked bars of different heights, each stack showing two subsets of a total set. In addition, the alternative answers required the candidates to choose the correct explanation of the reasoning involved in the identification of the stack in which a specified subset was the smallest fraction. The question required writers to identify the subset that was ‘the smallest proportion of the total’. Only 34% of the candidates answered this item correctly (see Table 1). More than 50% of all candidates (and nearly 70% in the lowest quarter and 31% in the top quarter) chose answers that reflected reasoning with absolute quantities rather than relative quantities. These candidates ignored the word ‘proportion’ and effectively selected the smallest numerator (the shortest bar in the chart). In their literature review, Tourniaire and Pulos (1985, p. 185) noted that this strategy of simply comparing the numerators (and ignoring the denominators) is ‘a developmentally primitive strategy’, but that ‘it is still used with some frequency in adolescence’. We have also seen that this strategy is used by about half of the students in a university quantitative literacy course for law students (Lloyd & Frith, 2013). The results for Question 7 reveal that even in the top quarter, under two-thirds of the candidates could successfully compare fractions by reasoning alone (admittedly in a fairly complex, reading-intensive question). In comparing the performance in Question 6 and Question 7 (58% and 34% of candidates answering correctly, respectively), it once again appears that the graphical presentation of the data and the alternatives being in a less familiar format than the numerical representation have affected performance adversely.
Comparison problems (comparing denominators)
While Questions 4 to 7 were more traditional comparison problems requiring the comparison of the rates (the size of the fractions), Question 8 and Question 9 required the sizes of the denominators to be compared. They were presented in the same way as Question 4 and Question 5 (set in the context of speed-distance-time and crime rate respectively), but, this time, with the numerators and rates given. Thus in Question 8 four pairs of distance and speed values were given and the problem was to identify the longest time, while in Question 9 four pairs of numbers of crimes and crime rates were given and the problem was to identify the biggest population.
In both of these problems the performance was worse than in the equivalent problems requiring comparison of the rates (see Table 1). Only 51% of all candidates answered Question 8 correctly (compared to 78% for Question 4) and only 25% answered Question 9 correctly (compared to 65% for Question 5). It is clear that this change to the structure of the problems has made them much more difficult. In addition, the (perhaps) less familiar context of crime rate made Question 9 more difficult than Question 8 which used the context of speed-distance-time. We do, however, recognise that Question 9 was the second last item in a very long test and the number of candidates who left it out was greater than for other items.
In Question 8 the alternative that represented the largest speed and largest distance (C) was the second most popular choice after the correct answer. The equivalent (incorrect) alternative was even more frequently chosen in Question 9, where the one representing the largest rate and largest numerator (B) was chosen by 41% (compared to 25% choosing the correct alternative). For this question it was only in the highest performance band where more candidates (45%) chose the correct answer than alternative B (33%), and even in this case it was not the majority (see Figure 3). The other alternative that was more popular than the correct answer with the lower performance bands was D, which represented fewer crimes and a bigger crime rate.
 |
FIGURE 3: Results for comparison problems requiring the comparison of the denominators, by performance band. |
|
It is clear from these results that the structure of these comparison problems affects difficulty. Although we have not found evidence of research on this type of problem, research on missing value problems has shown that the position in the fraction (numerator or denominator) of the number to be found affects the difficulty (Conner et al., 1988). In a similar way, we see that when the focus is on the denominators the comparison problem becomes more difficult than when the focus is on the fraction as a whole.
We are confident that the large sample lends credibility to our observations, but we acknowledge that there are shortcomings in both the format of the questions and the form of the data used for analysis. The format of multiple choice questions could impact the performance of candidates with little experience in this form of assessment. Also, the data consists only of the quantitative results of students’ performance on a limited number of multiple choice questions written at the end of a long test. Clearly, the data would benefit from being supplemented by qualitative information, but this was beyond the scope of this study.
Conclusion
It is widely accepted across different levels of the education sector that quantitative literacy is important for critical citizenship, a feature of which is the ability to engage confidently with social and other data. Appropriate application of proportional reasoning is often essential for gaining a full understanding of data in society and is also an important requirement for many academic disciplines.
This study has shown that many students aspiring to higher education perform poorly on proportional reasoning questions. This is not wholly unexpected in light of the literature reporting, on the proportional reasoning abilities of mainly young children and early adolescents. However some of the difficulties experienced were greater than we anticipated. Only approximately 80% of candidates could identify the correct answer to the simplest question involving calculating a missing value in a highly familiar context using easy numbers. In some questions requiring more complex proportional reasoning, less than half could answer correctly.
Two factors that we have seen to affect the difficulty of proportional reasoning problems are the context and structure of the question. Embedded in the notion of context are issues of familiarity with the event in which the task is situated and the associated language required to describe the event and the task, as well as the types of numbers used. Our study indicated that contexts that are likely to be less familiar to candidates, or are more complex in terms of number type or language demands, make problems more difficult.
The structure of a problem includes the type of problem in which quantities are to be reasoned about (missing value or comparison), whether there is coordination of the measure spaces and the location of the missing value. The performance on missing value and comparison types in comparable contexts is similar, but, in the case of comparison problems the difficulty is influenced by the location of the quantity to be reasoned about: whether it is the denominator or the fraction itself. In both missing value and comparison problems the representation of the answers, as mathematical expressions or as sentences that explain the reasoning involved, has the most adverse effect on performance. This appears to indicate that many candidates lacked a conceptual understanding of the mathematics involved.
The vast body of literature indicates that the development of proportional reasoning requires repeated exposure to problems in a variety of contexts over a long period of time. Although the curricula for Mathematics and Mathematical Literacy specify dealing with proportions, the explicit teaching of this does not go beyond Grade 9 (in the case of Mathematics) or Grade 10 (in the case of Mathematical Literacy). The emphasis appears to be on solving missing value problems where calculations are done, presumably, using a calculator and by means of a learned algorithm.
The results of this study support the existing research that shows that the intentional development of proportional reasoning should begin in the intermediate phase and continue into late adolescence and beyond, in the case of higher education. A greater focus needs to be on reasoning about proportions (rather than application of algorithms), in different contexts, with exposure to a variety of ways of presenting problems, in terms of both the language used and the representation of the data provided. Opportunities for the development and practice of this kind of reasoning should be exploited at all levels across the curriculum.
Acknowledgement
We thank the NBT project team at the Centre for Educational Testing for Access and Placement at the University of Cape Town who provided the opportunity to conduct this research, with the goal of contributing to the NBT project’s purpose of assessing the relationship between entry level proficiencies and school-level exit outcomes.
Authors’ contributions
Both authors contributed equally to the conceptualisation and realisation of the research project and the writing of the article.
Competing interests
The authors declare that they have no financial or personal relationship(s) that may have inappropriately influenced them in writing this article.
References
Bell, A., Fischbein, E., & Greer, B. (1984). Choice of operation in verbal arithmetic problems: The effects of number size, problem structure and context. Educational Studies in Mathematics, 15, 129–147.
Chapman, A., & Lee, A. (1990). Rethinking literacy and numeracy. Australian Journal of Education, 34(3), 277–289.
Conner, G., Harel, G., & Behr, M. (1988). The effect of structural variables on the level of difficulty of missing value proportion problems. In M. Behr, C. Lacampagne, & M. Wheeler (Eds.), Proceedings of the Tenth Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 65–71). DeKalb, IL: PME. Available from http://www.cehd.umn.edu/ci/rationalnumberproject/88_4.html
Courtney-Clarke, M., & Wessels, H. (2014). Number sense of final year pre-service primary school teachers. Pythagoras, 35(1). Article #244, 9 pages. http://dx.doi.org/10.4102/pythagoras.v35i1.244
Cramer, K., Post, T., & Currier, S. (1993). Learning and teaching ratio and proportion: Research implications. In D. Owens (Ed.), Research ideas for the classroom (pp. 159–178). New York, NY: Macmillan Publishing Company. Available from http://www.cehd.umn.edu/ci/rationalnumberproject/93_4.html
Department of Basic Education. (2011a). National curriculum statement. Curriculum and Assessment Policy Statement Grades 7–9. Mathematics. Pretoria: DBE. Available from http://www.education.gov.za/LinkClick.aspx?fileticket=uCNqOwfGbmc%3d&tabid=573&mid=1629
Department of Basic Education. (2011b). National curriculum statement. Curriculum and Assessment Policy Statement Grades 10–12. Mathematical Literacy. Pretoria: DBE. Available from http://www.education.gov.za/LinkClick.aspx?fileticket=q8%2bSkGy43rw%3d&tabid=570&mid=1558
Frith, V., & Lloyd, P. (2014). Students’ difficulty with proportional reasoning in a university quantitative literacy course. South African Journal of Higher Education, 28(3), 940–960.
Frith, V., & Prince, R.N. (2006). Quantitative literacy. In H. Griesel (Ed.), Access and entry-level benchmarks: The National Benchmark Tests Project (pp. 28–34). Pretoria: Higher Education South Africa. Available from http://www.universitiessa.ac.za/sites/www.universitiessa.ac.za/files/2006_HESA_Access%20and%20Entry%20Level%20Benchmarks_0.pdf
Gal, I., Van Groenestijn, M., Manly, M., Schmitt, M.J., & Tout, D. (2005). Adult numeracy and its assessment in the ALL Survey: A conceptual framework and pilot results. In T. Scott Murray, Y. Clermont, & M. Binkley (Eds.), Measuring adult literacy and life skills: New frameworks for assessment (pp. 137–191). Ottawa: Statistics Canada. Available from http://www.statcan.gc.ca/pub/89-552-m/89-552-m2005013-eng.pdf
Harel, G., & Behr, M. (1989). Structure and hierarchy of missing value proportion problems and their representations. Journal of Mathematical Behavior, 8(1), 77–119.
Harel, G., Behr, M., Post, T., & Lesh, R. (1991). Variables affecting proportionality: Understanding of physical principles, formation of quantitative relations and multiplicative invariance. In F. Furinghetti (Ed.), Proceedings of 15th Conference of the International Group for the Psychology of Mathematics Education (Vol. 2, pp. 125–133). Assisi, Italy: PME. Available from http://www.cehd.umn.edu/ci/rationalnumberproject/91_2.html
Harries, C., & Botha, J. (2013). Assessing medical students’ competence in calculating drug doses. Pythagoras, 34(2) Article #186, 9 pages. http://dx.doi.org/10.4102/pythagoras.v34i2.186
Heller, P., Post, T., & Behr, M. (1985). The effect of rate type, problem setting and rational number achievement on seventh grade students’ performance on qualitative and numerical proportional reasoning problems. In S. Damarin, & M. Shelton (Eds.), Proceedings of the Seventh Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (pp. 113–122). Columbus, OH: PME. Available from http://www.cehd.umn.edu/ci/rationalnumberproject/85_2.html
Inhelder, B., & Piaget, J. (1958). The growth of logical thinking from childhood to adolescence. London: Routledge and Kegan Paul.
Jablonka, E. (2003). Mathematical literacy. In A.J. Bishop, M.A. Clements, C. Keitel, J. Kilpatrick, & F.K.S. Leung (Eds.), Second international handbook of mathematics education (pp. 75–102). Dordrecht: Kluwer Academic.
Johnston, B. (2007). Critical numeracy? In S. Kelly, B. Johnston, & K. Yasukawa (Eds.), The adult numeracy handbook. Reframing adult numeracy in Australia (pp. 50–56). Sydney: Adult Literacy and Numeracy Australian Research Consortium.
Lamon, S.J. (2007). Rational numbers and proportional reasoning: Towards a theoretical framework for research. In F.K. Lester (Ed.), Second handbook of research on mathematics teaching and learning (pp. 629–667). Charlotte, NC: Information Age Publishing.
Lawton, C.A. (1993). Contextual factors affecting errors in proportional reasoning. Journal for Research in Mathematics Education, 24(5), 460–466.
Lesh, R., Post, T., & Behr, M. (1988). Proportional reasoning. In J. Hiebert, & M. Behr (Eds.), Number concepts and operations in the middle grades (pp. 93–118). Reston, VA: NCTM. Available from http://www.cehd.umn.edu/ci/rationalnumberproject/88_8.html
Lloyd, P., & Frith, V. (2013). Proportional reasoning as a threshold to numeracy at university: A framework for analysis. Pythagoras, 34(2) Article #234, 9 pages. http://dx.doi.org/10.4102/pythagoras.v34i2.234
Meyer, J.H.F., & Land, R. (2003) Threshold concepts and troublesome knowledge: Linkages to ways of thinking and practising within the disciplines. Enhancing Teaching-Learning Environments in Undergraduate Courses Project, Occasional Report 4. Edinburgh: University of Edinburgh. Available from http://www.etl.tla.ed.ac.uk/docs/ETLreport4.pdf
Steen, L.A. (2004). Achieving quantitative literacy: An urgent challenge for higher education. Washington, DC: Mathematical Association of America.
Thornton, M.C., & Fuller, R. (1981). How do college students solve proportion problems? Robert G. Fuller Publications and Presentations. Paper 24. Lincoln: University of Nebraska Digital Commons. Available from http://digitalcommons.unl.edu/physicsfuller/24
Tourniaire, F., & Pulos, S. (1985). Proportional reasoning: A review of the literature. Educational Studies in Mathematics, 16, 181–204.
Van den Heuvel-Panhuizen, M. (2005). The role of contexts in assessment problems in mathematics. For the Learning of Mathematics, 25(2), 2–9, 23. Available from http://www.jstor.org/stable/40248489
|